Exam 13: Inference in Linear Models
Exam 1: Basic Ideas39 Questions
Exam 2: Graphical Summaries of Data40 Questions
Exam 3: Numerical Summaries of Data76 Questions
Exam 4: Summarizing Bivariate Data33 Questions
Exam 5: Probability99 Questions
Exam 6: Discrete Probability Distributions76 Questions
Exam 7: The Normal Distribution131 Questions
Exam 8: Confidence Intervals62 Questions
Exam 9: Hypothesis Testing115 Questions
Exam 10: Two-Sample Confidence Intervals44 Questions
Exam 11: Two-Sample Hypothesis Tests43 Questions
Exam 12: Tests With Qualitative Data26 Questions
Exam 13: Inference in Linear Models51 Questions
Exam 14: Analysis of Variance48 Questions
Exam 15: Nonparametric Statistics27 Questions
Select questions type
Use the given set of points to construct a 95% confidence interval for .
x 8 6 5 9 6 12 14 11 y 21 18 15 21 21 28 28 24
(Multiple Choice)
4.9/5  (40)
(40)
The following table lists values measured for 10 consecutive eruptions of the geyser Old Faithful in Yellowstone National Park. They are the duration, in minutes, of the eruption , the dormant Period before the eruption , and the dormant period after the eruption (y).
y 3.5 80 84 4.1 84 50 2.3 50 93 4.7 93 55 1.7 55 76 4.9 76 58 1.7 58 74 4.6 74 75 3.4 75 80 4.3 80 56
Construct the multiple regression equation =b0+b1x1+b2x2
(Multiple Choice)
4.8/5  (50)
(50)
Use the given set of points to compute the margin of error for a 95% confidence interval for .
x 9 9 13 7 9 14 8 10 y 18 23 27 19 24 35 19 25
(Multiple Choice)
4.7/5  (37)
(37)
Use the given set of points to compute the predicted value
for the given value of x.
x 13 14 16 13 13 16 y 61 66 75 60 64 72 x=12
(Multiple Choice)
4.9/5  (40)
(40)
Use the given set of points to compute b0 and b1.
x 16 12 14 19 18 10 y 74 58 62 82 82 49 xequals12
(Multiple Choice)
4.9/5  (30)
(30)
Construct the multiple regression sequence =b0+b1x1+b2x2+b3x3 for the following data set:
y 51.0 80 34 7.5 34.3 60 22 2.5 31.5 60 24 5.0 33.2 60 23 4.0 49.2 60 29 6.5 46.7 70 27 7.5 30.4 70 32 4.0 43.2 60 25 5.5 30.6 60 26 3.5 43.3 70 28 7.5
(Multiple Choice)
4.8/5  (40)
(40)
Use the given set of points to compute the sum of squares for x,(x- . x 13 13 20 16 12 20 y 55 59 89 72 56 85 x=17
(Multiple Choice)
4.9/5  (34)
(34)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 6 subjects. Times were measured in thousandths of A second. The results are presented in the following table. The following MINITAB output describes the fit of a linear model to these data. Assume that the ass of the linear model are satisfied.
The regression equation is Auditory Visual
Predictor Coef SE Coef T P Constant 204.285245 10.451581 19.54587 0.000041 Visual 0.286943 0.051998 5.518383 0.005265 What is the intercept of the least-squares regression line?
(Multiple Choice)
4.7/5  (33)
(33)
The following display from a TI-84 Plus calculator presents the results of a test of the null hypothesis  How many degrees of freedom did the calculator use?
How many degrees of freedom did the calculator use?
(Multiple Choice)
4.8/5  (37)
(37)
The following MINITAB output presents a multiple regression equation .
The regression equation is
Predictor Coef SE Coef T P Constant 5.3535 0.7240 0.8771 0.338 X1 0.7929 0.7986 3.3073 0.002 X2 -0.8918 0.8208 -2.9354 0.009 X3 0.5297 0.8980 1.9458 0.083 X4 -1.7948 0.6461 -1.0262 0.340
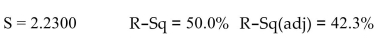 Source DF SS MS F P Regression 4 1,188.8 297.2 7.7396 0.003 Residual Error 31 1,190.1 38.4 Total 35 2,378.9
b3x3 What percentage of the variation in y is explained by the model?
Source DF SS MS F P Regression 4 1,188.8 297.2 7.7396 0.003 Residual Error 31 1,190.1 38.4 Total 35 2,378.9
b3x3 What percentage of the variation in y is explained by the model?
(Multiple Choice)
4.8/5  (32)
(32)
The following MINITAB output presents a multiple regression equation .
The regression equation is
Predictor Coef SE Coef T P Constant 1.9568 0.8248 1.1277 0.345 X1 1.7369 0.7980 3.4296 0.004 X2 1.1099 0.7500 -3.2529 0.006 X3 -1.2672 0.7534 1.8730 0.076 X4 1.6080 0.8733 -0.9328 0.349
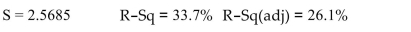 Source DF SS MS F P Regression 4 503.9 126.0 5.0806 0.003 Residual Error 40 990.4 24.8 Total 44 1,494.3
Predict the value of when
Source DF SS MS F P Regression 4 503.9 126.0 5.0806 0.003 Residual Error 40 990.4 24.8 Total 44 1,494.3
Predict the value of when
(Multiple Choice)
4.8/5  (40)
(40)
The following MINITAB output presents a 95% confidence interval for the mean ozone level on days when the relative humidity is 55%, and a 95% prediction interval for the ozone level on a Particular day when the relative humidity is 55%. The units of ozone are parts per billion. Predicted Values for New Observations
New Obs Fit SE Fit 95.0\% CI 95.0\% PI 1 38.46 1.4 (35.72,41.20) (22.17,54.75)
 What is the point estimate for the mean ozone level for days when the relative humidity is ?
What is the point estimate for the mean ozone level for days when the relative humidity is ?
(Multiple Choice)
4.7/5  (39)
(39)
The summary statistics for a certain set of points are: , and . Assume the conditions of the linear model hold. A confidence interval for will be constructed. What is the critical value?
(Multiple Choice)
4.9/5  (44)
(44)
Use the given set of points to compute the standard error of , . x 5 15 12 6 8 10 5 14 y 15 37 28 18 22 26 13 33
(Multiple Choice)
4.7/5  (34)
(34)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths Of a second. The results are presented in the following table.
Visual Auditory 208 200 177 175 250 233 248 234 152 155 164 161 196 190 238 230
Compute the least-squares regression line for predicting auditory response time (y) from visual response Time (x).
(Multiple Choice)
4.8/5  (35)
(35)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths of A second. The results are presented in the following table.
Visual Auditory 201 241 164 237 189 243 168 243 190 244 239 247 169 237 236 244
Construct a 99% confidence interval for the mean auditory response time for subjects with a visual Response time of 171.
(Multiple Choice)
4.9/5  (31)
(31)
The summary statistics for a certain set of points are: , and Assume the conditions of the linear model hold. A 99% confidence interval for will be constructed.
Test the null hypothesis versus . Use the level of significance.
(Multiple Choice)
4.9/5  (30)
(30)
The following MINITAB output presents a multiple regression equatior =b0+b1x1+b2x2+b3x3+b4x4
The regression equation is
Predictor Coef SE Coef T P Constant 2.5919 0.6269 1.1668 0.337 X1 -1.3391 0.6716 3.5190 0.002 X2 0.6212 0.8488 -3.2848 0.004 X3 1.6435 0.7934 1.8821 0.090 X4 1.4269 0.7679 -0.9879 0.345
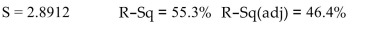 Source DF SS MS F P Regression 4 735.9 184.0 7.7311 0.003 Residual Error 25 594.6 23.8 Total 29 1,330.5
Let be the coefficient Test the hypothesis versus level. What do you conclude?
Source DF SS MS F P Regression 4 735.9 184.0 7.7311 0.003 Residual Error 25 594.6 23.8 Total 29 1,330.5
Let be the coefficient Test the hypothesis versus level. What do you conclude?
(Multiple Choice)
4.8/5  (37)
(37)
Use the given set of points to compute the residual standard deviation x 13 10 10 11 13 7 11 6 y 32 26 23 24 28 16 26 21
(Multiple Choice)
4.8/5  (41)
(41)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 6 subjects. Times were measured in thousandths of A second. The results are presented in the following table.
The following MINITAB output describes the fit of a linear model to these data. Assume that the assumptions Of the linear model are satisfied. The regression equation is Auditory Visual
Predictor Coef SE Coef T P Constant 212.498779 26.573957 7.996505 0.001327 Visual 0.245553 0.124489 1.972495 0.119828 Can you conclude that the response time to visual stimulus is useful in predicting the response time for Auditory stimulus? Answer this question using the α = 0.05 level of significance.
(True/False)
4.9/5  (38)
(38)
Showing 21 - 40 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)