Exam 2: Parallel Lines
Exam 1: Line and Angle Relationships13 Questions
Exam 2: Parallel Lines13 Questions
Exam 3: Triangles16 Questions
Exam 4: Quadrilaterals14 Questions
Exam 5: Similar Triangles12 Questions
Exam 6: Circles10 Questions
Exam 7: Locus and Concurrence4 Questions
Exam 8: Areas of Polygons and Circles5 Questions
Exam 9: Surfaces and Solids4 Questions
Exam 10: Analytical Geometry8 Questions
Exam 11: Introduction to Trigonometry4 Questions
Exam 12: Geometry Problems: Complementary Angles, Collinear Points, and Similar Triangles916 Questions
Select questions type
Use an indirect proof to complete the following problem.
Given: 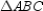 (not shown)
Prove:
(not shown)
Prove:  and
and 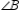 cannot both be right angles.
cannot both be right angles.
Free
(Essay)
4.9/5  (30)
(30)
Correct Answer:
Suppose that  and
and 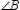 are both be right angles. Then
are both be right angles. Then 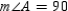 and
and 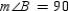 .
.
By the Protractor Postulate, 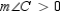 . Then
. Then 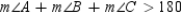 . But this last
. But this last
statement contradicts the fact that the sum of teh three interior angles of a triangle is exactly 180. Thus, the supposition must be false and it follows that  and
and 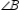 cannot both be right angles.
cannot both be right angles.
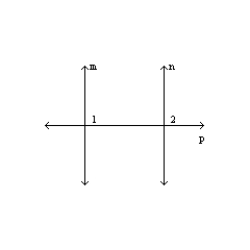 -Supply missing statements and missing reasons for the following proof.
Given:
-Supply missing statements and missing reasons for the following proof.
Given: 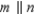 and transversal p;
and transversal p; 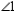 is a right angle
Prove:
is a right angle
Prove:  is a right angle
S1.
is a right angle
S1.  and transversal p R1.
S2.
and transversal p R1.
S2. 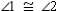 R2.
S3. R3. Congruent measures have equal measures.
S4.
R2.
S3. R3. Congruent measures have equal measures.
S4. 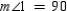 R4.
S5. R5. Substitution Property of Equality
S6. R6. Definition of a right angle
R4.
S5. R5. Substitution Property of Equality
S6. R6. Definition of a right angle
Free
(Essay)
4.8/5  (39)
(39)
Correct Answer:
R1. Given
R2. If 2 parallel lines are cut by a trans, corresponding angles are congruent.
S3. 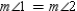 R4. Given
R4. Given
S5. 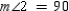 S6.
S6.  is a right angle
is a right angle
Use an indirect proof to complete the following problem.
Given: 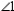 and
and  are supplementary (no drawing)
Prove:
are supplementary (no drawing)
Prove: 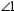 and
and  are not both obtuse angles.
are not both obtuse angles.
Free
(Essay)
4.9/5  (31)
(31)
Correct Answer:
Suppose that 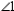 and
and  are both obtuse angles. Then
are both obtuse angles. Then 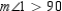 and
and 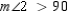 .
.
It follows that 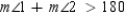 . But it is given that
. But it is given that 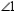 and
and  are supplementary, so that
are supplementary, so that 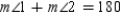 .
.
With a contradiction of the known fact, it follows that the supposition must be false; thus,  and
and  are not both obtuse angles.
are not both obtuse angles.
 -Supply missing statements and reasons for the foloowing proof.
Given:
-Supply missing statements and reasons for the foloowing proof.
Given:  is supplementary to
is supplementary to  Prove:
Prove: 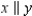 S1. R1.
S2.
S1. R1.
S2.  is supp. to
is supp. to  R2. If the ext. sides of 2 adj. angles form a line, the angles are supp.
S3. R3. Angles supp. to the same angle are congruent.
S4. R4.
R2. If the ext. sides of 2 adj. angles form a line, the angles are supp.
S3. R3. Angles supp. to the same angle are congruent.
S4. R4.
(Essay)
4.8/5  (39)
(39)
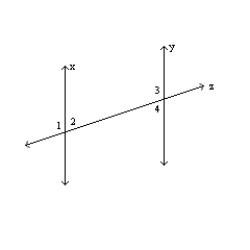
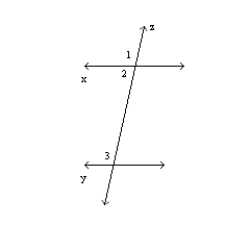 -In the figure, x || y and transversal z. Explain why
-In the figure, x || y and transversal z. Explain why  and
and  must be supplementary.
must be supplementary.
(Essay)
4.9/5  (38)
(38)
Explain the following statement.
The measure of each interior angle of an equiangular triangle is 60.
(Essay)
4.8/5  (31)
(31)
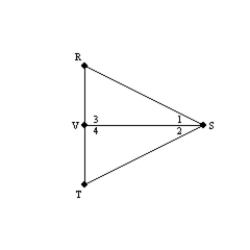 -Supply missing statements and missing reasons for the following proof.
Given:
-Supply missing statements and missing reasons for the following proof.
Given: 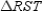 so that
so that 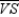 bisects
bisects 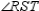 ;
also,
;
also, 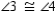 Prove:
Prove: 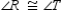 S1.
S1. 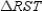 so that
so that 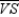 bisects
bisects 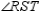 R1.
S2. R2.
S3. R3. Given
S4. R4. If 2 angles of one triangle are congruent to
2 angles of a second triangle, then the third angles
of these triangles are also congruent.
R1.
S2. R2.
S3. R3. Given
S4. R4. If 2 angles of one triangle are congruent to
2 angles of a second triangle, then the third angles
of these triangles are also congruent.
(Essay)
4.7/5  (34)
(34)
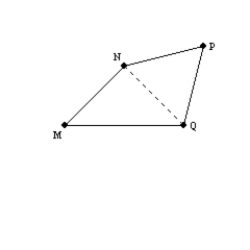 -Using the drawing provided, explain the following statement.
The sum of the interior angles of a quadrilateral is 360.
-Using the drawing provided, explain the following statement.
The sum of the interior angles of a quadrilateral is 360.
(Essay)
4.8/5  (38)
(38)
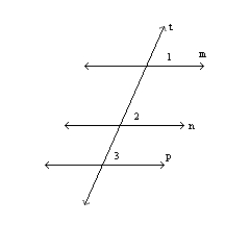 -Supply missing statements in the following proof.
Given:
-Supply missing statements in the following proof.
Given:  and
and  Prove:
Prove: 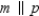 S1. R1. Given
S2. R2. If 2 parallel lines are cut by a transversal, corr. angles are congruent.
S3. R3. Given
S4. R4. Same as #2.
S5. R5. Transitive Property of Congruence
S6. R6. If 2 lines are cut by a transversal so that corresponding angles
are congruent, then these lines are parallel.
S1. R1. Given
S2. R2. If 2 parallel lines are cut by a transversal, corr. angles are congruent.
S3. R3. Given
S4. R4. Same as #2.
S5. R5. Transitive Property of Congruence
S6. R6. If 2 lines are cut by a transversal so that corresponding angles
are congruent, then these lines are parallel.
(Essay)
4.8/5  (33)
(33)
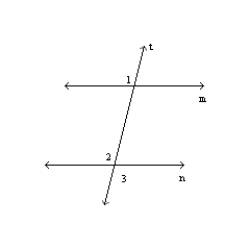 -Supply missing reasons for this proof.
Given: m || n
Prove:
-Supply missing reasons for this proof.
Given: m || n
Prove: 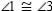 S1. m || n R1.
S2.
S1. m || n R1.
S2. 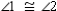 R2.
S3.
R2.
S3. 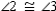 R3.
S4.
R3.
S4. 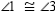 R4.
R4.
(Essay)
4.9/5  (32)
(32)
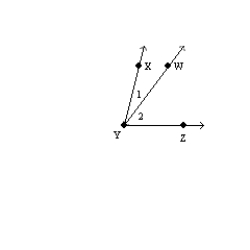 -Use an indirect proof to complete the following problem.
Given:
-Use an indirect proof to complete the following problem.
Given: 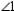 is not congruent to
is not congruent to  Prove:
Prove: 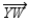 does not bisect
does not bisect 
(Essay)
4.8/5  (34)
(34)
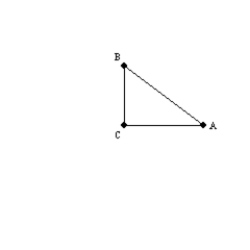 -In the triangle shown,
-In the triangle shown,  is a right angle.Explain why
is a right angle.Explain why  and
and  are complementary.
are complementary.
(Essay)
4.7/5  (28)
(28)
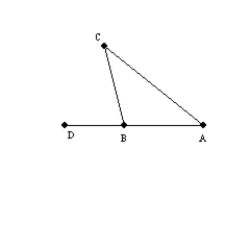 -Supply missing reasons for the following proof.
Given:
-Supply missing reasons for the following proof.
Given: 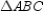 with D-B-A
Prove:
with D-B-A
Prove: 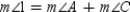 S1.
S1. 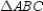 with D-B-A R1.
S2.
with D-B-A R1.
S2. 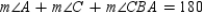 R2.
S3.
R2.
S3. 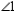 and
and 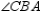 are supp. R3.
S4.
are supp. R3.
S4. 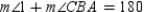 R4.
S5.
R4.
S5. 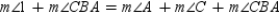 R5.
S6.
R5.
S6. 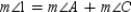 R6.
R6.
(Essay)
4.7/5  (26)
(26)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)