Exam 4: Applications of the Derivative
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Find the relative maxima and relative minima, if any, of the function. Otherwise, answer none.
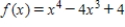
Relative minima: __________
Relative maxima: __________
Relative minima: __________
Relative maxima: __________
(Short Answer)
4.7/5  (44)
(44)
The concentration (in milligrams/cubic centimeter) of a certain drug in a patient's body t hr after injection is given by 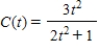
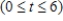 .
When is the concentration of the drug increasing, and when is it decreasing?
.
When is the concentration of the drug increasing, and when is it decreasing?
(Multiple Choice)
4.7/5  (35)
(35)
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 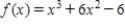 on
on 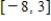
(Multiple Choice)
5.0/5  (36)
(36)
Find the horizontal and vertical asymptotes of the graph of the function. (You need not sketch the graph.)
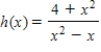
Horizontal asymptote(s) __________
Vertical asymptote(s) __________
Horizontal asymptote(s) __________
Vertical asymptote(s) __________
(Short Answer)
4.9/5  (36)
(36)
Determine the relative maxima and relative minima, if any. 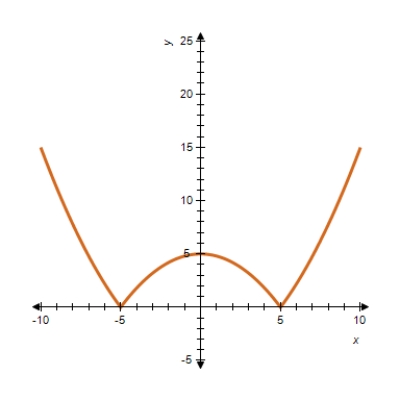
(Multiple Choice)
4.8/5  (40)
(40)
Phillip, the proprietor of a vineyard, estimates that the first 10,000 bottles of wine produced this season will fetch a profit of $2/bottle. However, the profit from each bottle beyond 10,000 drops by $0.0002 for each additional bottle sold. Assuming at least 10,000 bottles of wine are produced and sold, what is the maximum profit? Round the answer to two decimal places.
The maximum profit is $__________
What would be the price/bottle in this case? Round the answer to the nearest cent.
$__________/bottle
(Short Answer)
4.7/5  (39)
(39)
A stone is thrown straight up from the roof of an 48-ft building. The distance (in feet) of the stone from the ground at any time t (in seconds) is given by 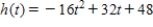 . Sketch the graph of h. When is the stone rising, and when is it falling? If the stone were to miss the building, when would it hit the ground?
. Sketch the graph of h. When is the stone rising, and when is it falling? If the stone were to miss the building, when would it hit the ground?
(Multiple Choice)
4.8/5  (41)
(41)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 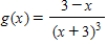
(Multiple Choice)
4.8/5  (32)
(32)
Find the inflection points, if any, of the following function. Otherwise, answer no solution.
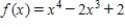
(Short Answer)
4.9/5  (38)
(38)
A manufacturer of tennis rackets finds that the total cost 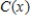 (in dollars) of manufacturing
(in dollars) of manufacturing  rackets/day is given by
rackets/day is given by 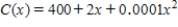 . Each racket can be sold at a price of
. Each racket can be sold at a price of 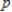 dollars, where
dollars, where 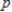 is related to
is related to  by the demand equation
by the demand equation 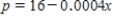 .
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
__________ rackets/day
.
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
__________ rackets/day
(Short Answer)
4.8/5  (32)
(32)
Find the relative maxima and relative minima, if any, of the function. 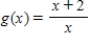
(Multiple Choice)
4.8/5  (37)
(37)
Find the horizontal and vertical asymptotes of the graph. 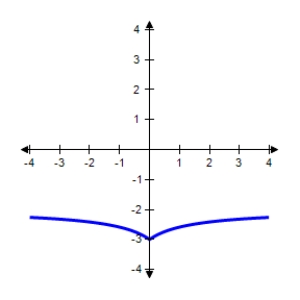
(Multiple Choice)
4.8/5  (29)
(29)
An apple orchard has an average yield of 36 bushels of apples/tree if tree density is 24 trees/acre. For each unit increase in tree density, the yield decreases by 3 bushels. How many trees should be planted in order to maximize the yield?
__________ trees
(Short Answer)
4.7/5  (43)
(43)
The graph of the function f shown in the accompanying figure gives the elevation of that part of the Boston Marathon course that includes the notorious Heartbreak Hill. Determine the intervals (stretches of the course) where the function f is increasing (the runner is laboring), where it is constant (the runner is taking a breather), and where it is decreasing (the runner is coasting). 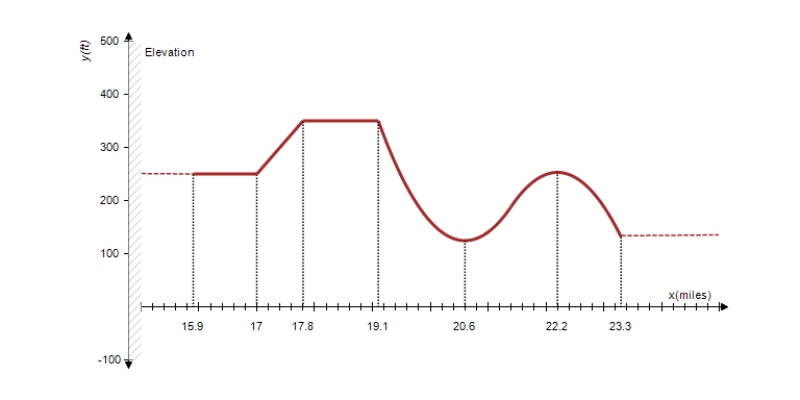
(Multiple Choice)
4.9/5  (33)
(33)
Find the relative maxima and relative minima, if any, of the function. 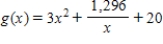
(Multiple Choice)
4.9/5  (42)
(42)
The quantity demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, manufactured by Phonola Record Industries, is related to the price/compact disc. The equation 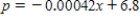
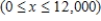 , where
, where 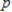 denotes the unit price in dollars and
denotes the unit price in dollars and  is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging
is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging  copies of this classical recording is given by
copies of this classical recording is given by 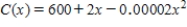
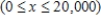 .
To maximize its profits, how many copies should Phonola produce each month?
.
To maximize its profits, how many copies should Phonola produce each month?
(Short Answer)
4.8/5  (38)
(38)
Find the interval(s) where each function is increasing and the interval(s) where it is decreasing. 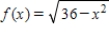
(Multiple Choice)
4.8/5  (47)
(47)
The total worldwide box-office receipts for a long-running movie are approximated by the function 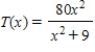
Where
Where 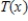 is measured in millions of dollars and x is the number of years since the movie's release.
Select the graph of the function T.
is measured in millions of dollars and x is the number of years since the movie's release.
Select the graph of the function T.
(Multiple Choice)
4.9/5  (42)
(42)
Showing 41 - 60 of 152
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)