Exam 4: Applications of the Derivative
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
A rectangular box is to have a square base and a volume of 4 ft.3. If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 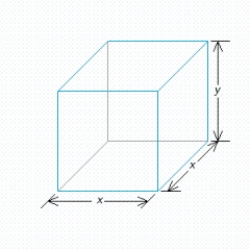
(Multiple Choice)
4.7/5  (32)
(32)
The average cost per disc (in dollars) incurred by Herald Records in pressing x DVDs is given by the average cost function
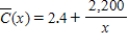
Find the horizontal asymptote of
Find the horizontal asymptote of 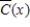 .
__________
What is the limiting value of the average cost?
__________
.
__________
What is the limiting value of the average cost?
__________
(Short Answer)
4.7/5  (42)
(42)
You are given the graph of a function
Determine the intervals where f is increasing, constant, or decreasing. 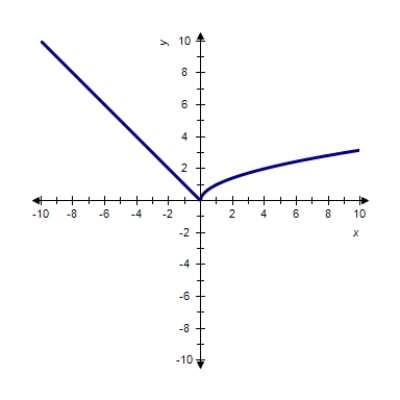
(Multiple Choice)
4.7/5  (43)
(43)
The quantity demanded each month of the Sicard wristwatch is related to the unit price by the equation 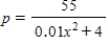
 , where
, where  is measured in dollars and
is measured in dollars and  is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
(Multiple Choice)
4.9/5  (38)
(38)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If  is increasing on
is increasing on 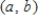 , then
, then 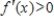 for each
for each  in
in 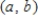 .
.
(Essay)
4.9/5  (39)
(39)
If an open box has a square base and a volume of 864 in.3 and is constructed from a tin sheet, find the dimensions of the box, assuming a minimum amount of material is used in its construction.
(Short Answer)
4.8/5  (34)
(34)
Find the relative maxima and relative minima of the function. 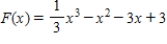
(Multiple Choice)
4.8/5  (28)
(28)
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 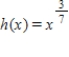
(Multiple Choice)
4.9/5  (33)
(33)
Find the horizontal and vertical asymptotes of the graph. 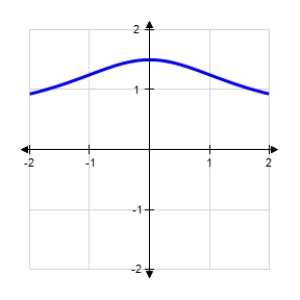
(Multiple Choice)
4.9/5  (43)
(43)
Use the information summarized in the table to select the graph of
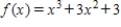 Domain:
Domain: 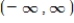 Intercept: y-intercept: 03 Asymptotes: None Intervals where f is ↑ and ↓: ↑ on
Intercept: y-intercept: 03 Asymptotes: None Intervals where f is ↑ and ↓: ↑ on 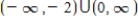 ↓ on
↓ on 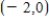 Relative extrema: Rel. min. at
Relative extrema: Rel. min. at 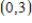 ; rel. ma. at
; rel. ma. at 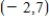 Concavity: Downward on
Concavity: Downward on 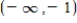 ; upward on
; upward on 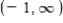 Point of inflection:
Point of inflection: 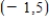
(Multiple Choice)
4.8/5  (46)
(46)
A truck gets 600/x mpg when driven at a constant speed of x mph (between 40 and 80 mph). If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 40 and 80 mph is it most economical to drive?
(Multiple Choice)
4.7/5  (33)
(33)
Select the graph of the function using the curve-sketching guide. 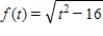
(Multiple Choice)
4.8/5  (47)
(47)
Find the relative maxima and relative minima, if any, of the function. 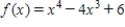
(Multiple Choice)
4.9/5  (42)
(42)
A stone is thrown straight up from the roof of a 90-ft building. The height (in feet) of the stone at any time t (in seconds), measured from the ground, is given by 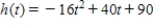
What is the maximum height the stone reaches?
What is the maximum height the stone reaches?
(Multiple Choice)
5.0/5  (40)
(40)
Find the horizontal and vertical asymptotes of the graph. 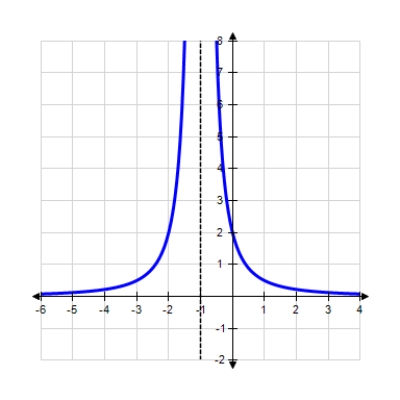
(Multiple Choice)
4.9/5  (39)
(39)
Find the horizontal and vertical asymptotes of the graph of the function. 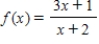
(Multiple Choice)
4.8/5  (39)
(39)
One of the functions below is the derivative function of the other. Identify each of them.
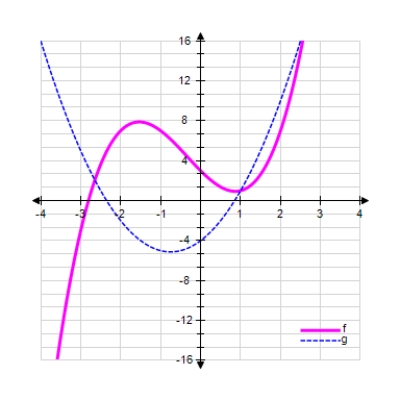
(Short Answer)
4.7/5  (33)
(33)
An apple orchard has an average yield of 30 bushels of apples/tree if tree density is 25 trees/acre. For each unit increase in tree density, the yield decreases by 2 bushels. How many trees should be planted in order to maximize the yield?
(Multiple Choice)
4.8/5  (37)
(37)
Showing 121 - 140 of 152
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)