Exam 4: Applications of the Derivative
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
What are the dimensions of a closed rectangular box that has a square cross section, a capacity of 127 in.3 and is constructed using the least amount of material? Round the answer to two decimal places.
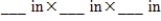
(Short Answer)
4.8/5  (28)
(28)
Suppose the total cost function for manufacturing a certain product is 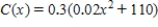 dollars, where
dollars, where  represents the number of units produced. Find the level of production that will minimize the average cost. Round the answer to the nearest integer.
represents the number of units produced. Find the level of production that will minimize the average cost. Round the answer to the nearest integer.
(Multiple Choice)
5.0/5  (39)
(39)
You are given the graph of a function
Determine the intervals where f is concave upward. 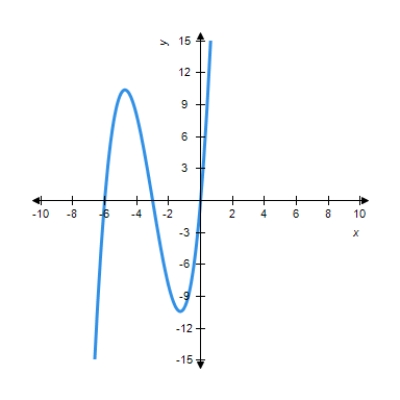
(Multiple Choice)
4.8/5  (27)
(27)
Find the horizontal and vertical asymptotes of the graph of the function. 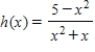
(Multiple Choice)
4.9/5  (41)
(41)
You are given the graph of some function f defined on the indicated interval. Find the absolute maximum and the absolute minimum of f, if they exist. 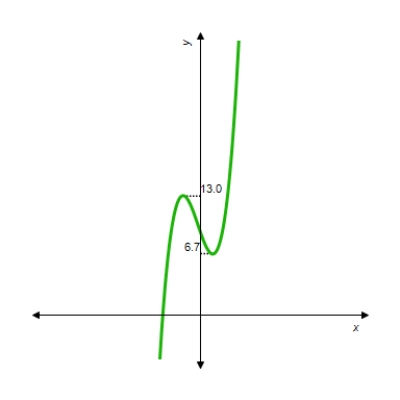 f defined on
f defined on 
(Multiple Choice)
4.9/5  (28)
(28)
The height (in feet) attained by a rocket t sec into flight is given by the function
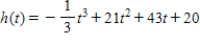 .
When is the rocket rising and when is it descending?
.
When is the rocket rising and when is it descending?
(Essay)
4.8/5  (41)
(41)
Find the horizontal and vertical asymptotes of the graph of the function. 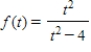
(Multiple Choice)
4.9/5  (34)
(34)
Determine the relative maxima and relative minima, if any. Otherwise, answer none.
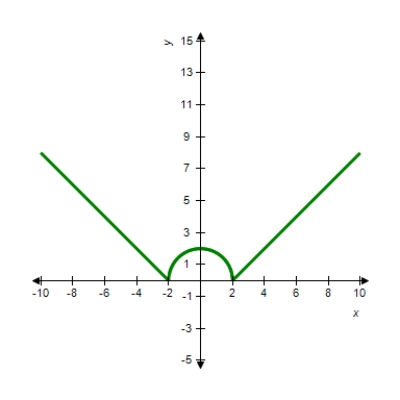
Relative maxima: __________
Relative minima: __________
Relative maxima: __________
Relative minima: __________
(Short Answer)
4.9/5  (39)
(39)
Use the information summarized in the table to select the graph of
 Domain:
Domain: 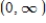 Intercepts: x-intercepts: 0, 4 Asymptotes: None Intervals where f is ↑ and ↓: ↑ on
Intercepts: x-intercepts: 0, 4 Asymptotes: None Intervals where f is ↑ and ↓: ↑ on 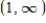 ↓ on
↓ on 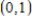 Relative extrema: Rel. min. at
Relative extrema: Rel. min. at 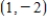 Concavity: Upward on
Concavity: Upward on 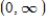 Point of inflection:
Point of inflection: 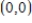
(Multiple Choice)
4.9/5  (48)
(48)
Postal regulations specify that a parcel sent by parcel post may have a combined length and girth of no more than 90 in.
Find the dimensions of a rectangular package that has a square cross section and the largest volume that may be sent through the mail.
(Short Answer)
4.9/5  (40)
(40)
A rectangular box is to have a square base and a volume of 24 ft.3. If the material for the base costs 20 cent/square foot, the material for the sides costs 10 cent/square foot, and the material for the top costs 40 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
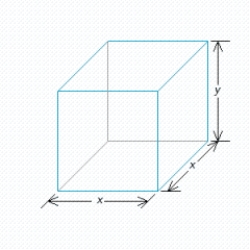

(Short Answer)
4.9/5  (38)
(38)
The level of ozone, an invisible gas that irritates and impairs breathing, present in the atmosphere on a certain May day in the city was approximated by
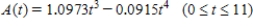 , where
, where 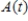 is measured in pollutant standard index (PSI) and t is measured in hours, with
is measured in pollutant standard index (PSI) and t is measured in hours, with 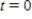 corresponding to 7
a.m. Use the second derivative test to show that the function A has a relative maximum at approximately
corresponding to 7
a.m. Use the second derivative test to show that the function A has a relative maximum at approximately 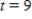 . Interpret your results.
. Interpret your results.
(Essay)
4.8/5  (41)
(41)
Showing 141 - 152 of 152
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)