Exam 11: Taylor Polynomials and Infinite Series
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Consider the series 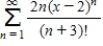 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.9/5  (31)
(31)
Find P3(x), the third Taylor polynomial of the following function at the indicated point.
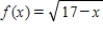 at
at 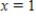
Express any non-integer coefficients as reduced fractions.
Express any non-integer coefficients as reduced fractions.
(Short Answer)
4.7/5  (36)
(36)
Use the integral test to determine whether the following series is convergent or divergent.
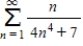
(Short Answer)
4.7/5  (38)
(38)
Estimate the value of the radical by using three iterations of the Newton-Raphson method with the indicated initial guess for the function. Round your answer to five decimal places, if necessary.
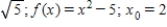
(Short Answer)
4.8/5  (40)
(40)
Use the Newton method to approximate the indicated zero of the function. Continue with the iteration until two successive approximations differ by less than 0.0001. Round your answer to five decimal places, if necessary.
The zero of 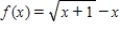 between
between 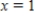 and
and 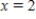 ,
, 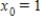 .
.
(Short Answer)
4.8/5  (27)
(27)
Determine whether the following p-series is convergent or divergent.
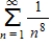
(Short Answer)
4.9/5  (42)
(42)
Consider the series
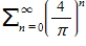 .
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
.
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
(Short Answer)
4.8/5  (35)
(35)
Use the comparison test to determine whether the series is convergent or divergent.
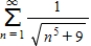
(Short Answer)
4.9/5  (49)
(49)
Use the integral test to determine whether the following series is convergent or divergent.
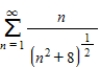
(Short Answer)
4.9/5  (35)
(35)
Consider the series 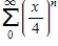 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.8/5  (31)
(31)
Find the Taylor series of the function at the indicated point. Give the interval of convergence for the series.
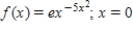
(Short Answer)
4.8/5  (42)
(42)
Find P4(x), the fourth Taylor polynomial of the following function at the indicated point.
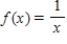 at
at 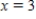
Express any non-integer coefficients as reduced fractions.
Express any non-integer coefficients as reduced fractions.
(Short Answer)
4.8/5  (40)
(40)
The proprietor of Qwik Film Lab recently purchased $12,400 of new film-processing equipment. She expects that this investment, which has a useful life of 4 yr, will yield returns of $4,400 at the end of the first year, $5,200 at the end of the second year, $4,300 at the end of the third year, and $3,100 at the end of the fourth year. Find the internal rate of return on the investment.
Round your answer to the nearest hundredth, if necessary.
__________ % per yr
(Short Answer)
4.9/5  (41)
(41)
Find the Taylor series of the function at the indicated point. Give the interval of convergence for the series.
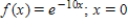
(Short Answer)
4.7/5  (31)
(31)
The temperature at 5 A.M. on a certain December day was measured at 18°F. In the next t hr, the temperature was given by the function
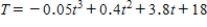
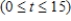
where T is measured in degrees Fahrenheit. At what time was the temperature 0 °F?
_____ : _____ P.M.
where T is measured in degrees Fahrenheit. At what time was the temperature 0 °F?
_____ : _____ P.M.
(Short Answer)
4.9/5  (27)
(27)
Use the integral test to determine whether the following series is convergent or divergent.
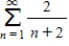
(Short Answer)
4.8/5  (43)
(43)
Consider the series
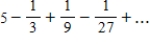 .
Determine whether the series converges or diverges.
If it converges, find its sum.
.
Determine whether the series converges or diverges.
If it converges, find its sum.
(Short Answer)
4.9/5  (33)
(33)
Consider the series
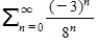 .
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
.
Determine whether the geometric series converges or diverges.
If it converges, find its sum.
(Short Answer)
4.8/5  (34)
(34)
Showing 41 - 60 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)