Exam 11: Taylor Polynomials and Infinite Series
Exam 1: Preliminaries183 Questions
Exam 2: Functions, Limits, and the Derivative250 Questions
Exam 3: Differentiation309 Questions
Exam 4: Applications of the Derivative152 Questions
Exam 5: Exponential and Logarithmic Functions256 Questions
Exam 6: Integration291 Questions
Exam 7: Additional Topics in Integration202 Questions
Exam 8: Calculus of Several Variables219 Questions
Exam 9: Differential Equations57 Questions
Exam 10: Probability and Calculus68 Questions
Exam 11: Taylor Polynomials and Infinite Series110 Questions
Exam 12: Trigonometric Functions64 Questions
Select questions type
Find P4(x), the fourth Taylor polynomial of the following function at the indicated point.
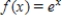 at
at 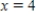
Express any non-integer coefficients as reduced fractions.
Express any non-integer coefficients as reduced fractions.
(Short Answer)
4.7/5  (34)
(34)
Consider the series 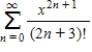 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.8/5  (40)
(40)
Determine whether the following p-series is convergent or divergent.
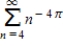
(Short Answer)
4.8/5  (33)
(33)
Find P3(x), the third Taylor polynomial of the following function at the indicated point.
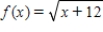 at
at 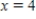
Express any non-integer coefficients as reduced fractions.
Express any non-integer coefficients as reduced fractions.
(Short Answer)
4.9/5  (28)
(28)
Executive Limousine Service recently acquired limousines worth $120,000. The projected returns over the next 3 yr, the time period the limousines will be in service, are $80,000 at the end of the first year, $60,000 at the end of the second year, and $40,000 at the end of the third year. Find the internal rate of return on the investment. Round your answer to the nearest hundredth, if necessary.
__________ % per year
(Short Answer)
4.8/5  (32)
(32)
Express the following decimal as a rational number.
2.251251251...
(Short Answer)
4.8/5  (28)
(28)
Use the Newton method to approximate the indicated zero of the function. Continue with the iteration until two successive approximations differ by less than 0.0001. Round your answer to four decimal places, if necessary.
The zero of 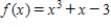 between
between 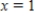 and
and 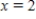 ,
, 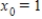 .
.
(Short Answer)
4.9/5  (36)
(36)
Consider the function 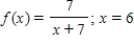 .
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
.
Find the Taylor series of the function at the indicated point.
__________
Find its radius of convergence.
__________
Find the interval of convergence.
__________
(Short Answer)
4.8/5  (38)
(38)
Use the Newton method to approximate the indicated zero of the function. Continue with the iteration until two successive approximations differ by less than 0.0001. Round your answer to six decimal places, if necessary.
The zero of 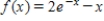 between
between 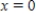 and
and 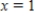 ,
, 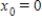 .
.
(Short Answer)
4.8/5  (34)
(34)
Determine whether the following series is convergent or divergent.
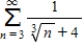
(Short Answer)
5.0/5  (31)
(31)
Differentiate the power series for 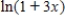 at
at 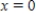 to obtain a series representation for the function
to obtain a series representation for the function 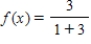 .
.
(Short Answer)
4.8/5  (38)
(38)
Use the integral test to determine whether the following series is convergent or divergent.
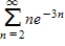
(Short Answer)
4.8/5  (30)
(30)
Use the Newton method to approximate the indicated zero of the function. Continue with the iteration until two successive approximations differ by less than 0.0001. Round your answer to five decimal places, if necessary.
The zero of 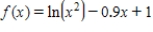 between
between 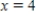 and
and 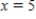 ,
, 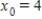 .
.
(Short Answer)
4.8/5  (43)
(43)
Find the Taylor series of the function at the indicated point. Give the interval of convergence for the series.
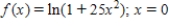
(Short Answer)
4.9/5  (33)
(33)
The General Manager of the Service Department of MCA Television Company has estimated that the time that elapses between the dates of purchase and the dates on which the 19-in. sets manufactured by the company first require service is normally distributed according to the probability density function
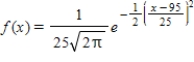
where x is measured in months. Determine the percentage of sets manufactured and sold by MCA that may require service 90-100 mo after purchase.
Round the answer to the nearest hundredth, if necessary.
__________%
where x is measured in months. Determine the percentage of sets manufactured and sold by MCA that may require service 90-100 mo after purchase.
Round the answer to the nearest hundredth, if necessary.
__________%
(Short Answer)
4.8/5  (29)
(29)
Consider the series 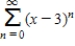 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.9/5  (40)
(40)
Find the Taylor series of the function at the indicated point. Give the interval of convergence for the series.
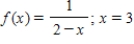
(Short Answer)
5.0/5  (43)
(43)
Consider the series 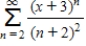 .
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
.
Find the radius of convergence of the power series.
__________
Find the interval of convergence of the power series.
__________
(Short Answer)
4.8/5  (34)
(34)
Of the microprocessors manufactured by a microelectronics firm for use in regulating fuel consumption in automobiles, 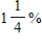 are defective. It can be shown that the probability of getting at least one defective microprocessor in a random sample of n microprocessors is
are defective. It can be shown that the probability of getting at least one defective microprocessor in a random sample of n microprocessors is 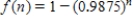 . Consider the sequence
. Consider the sequence 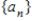 defined by
defined by 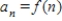 .
Write down the terms a1, a10, a100, and a1000 of the sequence
.
Write down the terms a1, a10, a100, and a1000 of the sequence 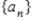 .
a1=__________
Round the answer to three decimal places, if necessary.
a10=__________
Round the answer to five decimal places, if necessary.
a100=__________
Round the answer to nine decimal places, if necessary.
a1000=__________
Round the answer to the nearest whole number, if necessary.
Evaluate
.
a1=__________
Round the answer to three decimal places, if necessary.
a10=__________
Round the answer to five decimal places, if necessary.
a100=__________
Round the answer to nine decimal places, if necessary.
a1000=__________
Round the answer to the nearest whole number, if necessary.
Evaluate 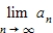 .
.
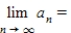 __________
__________
(Short Answer)
5.0/5  (42)
(42)
Use the integral test to determine whether the following series is convergent or divergent.
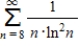
(Short Answer)
4.8/5  (32)
(32)
Showing 81 - 100 of 110
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)