Exam 8: Functions of Several Variables
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Suppose that 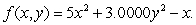 Find and classify (as local maxima, minima, or neither) all critical points of f.
Find and classify (as local maxima, minima, or neither) all critical points of f.
(Short Answer)
4.9/5  (32)
(32)
The fuel cost, C, for a 3000 mile trip depends on the price, p, per gallon of gasoline and fuel economy in miles per gallon, m, of the car according to the formula 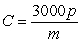 . On the same set of axes, sketch a graph of C as a function of m with fixed gas prices of $2.00, $2.25, $2.50, and $2.75. What do you observe as gas prices increase?
. On the same set of axes, sketch a graph of C as a function of m with fixed gas prices of $2.00, $2.25, $2.50, and $2.75. What do you observe as gas prices increase?
(Multiple Choice)
4.8/5  (35)
(35)
The function 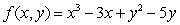 has a local minimum at (1, 2.5). Which of the following is a sketch of the level curves of f near this point?
has a local minimum at (1, 2.5). Which of the following is a sketch of the level curves of f near this point?
(Multiple Choice)
4.9/5  (33)
(33)
The number, N, of children that can be enrolled in a private school is a function of the number of certified teachers, T, and the number of aides, A, available, according to the formula 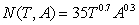 . Teachers average an annual salary of $38,000 and aides average an annual salary of $20,000. The annual budget for salaries is B = $800,000. If we want to maximize enrollment, which of the following is true?
. Teachers average an annual salary of $38,000 and aides average an annual salary of $20,000. The annual budget for salaries is B = $800,000. If we want to maximize enrollment, which of the following is true?
(Multiple Choice)
4.9/5  (33)
(33)
The quantity, Q, of a good produced depends on the number of workers, W, and the amount of capital invested, K, according to the Cobb-Douglas function 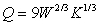 .
In addition, we know that labor costs are $19 per employee, capital costs are $8 per unit, and the budget is $2500. The maximum production level is about _____ units, where W = _____ and K = _____. Round to the nearest whole number.
.
In addition, we know that labor costs are $19 per employee, capital costs are $8 per unit, and the budget is $2500. The maximum production level is about _____ units, where W = _____ and K = _____. Round to the nearest whole number.
(Short Answer)
4.9/5  (38)
(38)
The critical point of 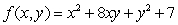 occurs at x = _____, y = _____, and is a local ________ (maximum / minimum / neither).
occurs at x = _____, y = _____, and is a local ________ (maximum / minimum / neither).
(Short Answer)
4.8/5  (28)
(28)
The quantity, Q, of a good produced depends on the quantities 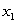 and
and 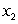 of the two main materials used:
of the two main materials used: 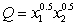 .
Material
.
Material 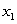 costs $55 per unit, and material
costs $55 per unit, and material 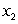 costs $70 per unit. We want to minimize the cost of producing 100 units of the good. Using Lagrange multipliers, we see that the minimum cost of ________ occurs when
costs $70 per unit. We want to minimize the cost of producing 100 units of the good. Using Lagrange multipliers, we see that the minimum cost of ________ occurs when 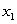 = _____ and
= _____ and 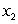 = _____.
= _____.
(Short Answer)
4.7/5  (33)
(33)
Two products are manufactured in quantities 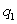 and
and 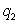 and sold at prices $8 and $12 respectively. The cost of producing them is given by
and sold at prices $8 and $12 respectively. The cost of producing them is given by 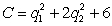 . Find the maximum profit that can be made.
. Find the maximum profit that can be made.
(Short Answer)
4.9/5  (48)
(48)
The production function for a company is 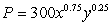 , where P is the amount produced given x units of labor and y units of equipment. Each unit of labor costs $900 and each unit of equipment costs $400. Assuming the goal of the company is to maximize production given a fixed budget of $40,000, what is the meaning of the Lagrange multiplier
, where P is the amount produced given x units of labor and y units of equipment. Each unit of labor costs $900 and each unit of equipment costs $400. Assuming the goal of the company is to maximize production given a fixed budget of $40,000, what is the meaning of the Lagrange multiplier 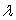 ?
?
(Multiple Choice)
4.7/5  (26)
(26)
Your monthly payment, C(s, t), on a car loan depends on the amount, s, of the loan (in thousands of dollars), and the time, t, required to pay it back (in months). Is C an increasing or decreasing function of t?
(Multiple Choice)
4.9/5  (37)
(37)
The quantity, Q, of a good produced depends on the quantities 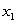 and
and 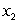 of the two main materials used:
of the two main materials used: 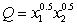 . Material
. Material 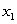 costs $100 per unit, and material
costs $100 per unit, and material 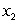 costs $25 per unit. We want to minimize the cost of producing 100 units of the good. What is the objective function?
costs $25 per unit. We want to minimize the cost of producing 100 units of the good. What is the objective function?
(Multiple Choice)
4.7/5  (37)
(37)
A table of values for 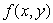 is given below. Estimate fy (8,10). Use the next higher point to make your estimate.
is given below. Estimate fy (8,10). Use the next higher point to make your estimate. 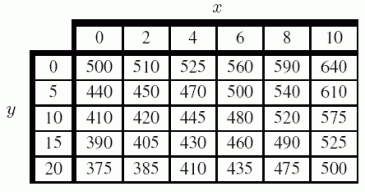
(Short Answer)
4.8/5  (47)
(47)
Find the critical points of 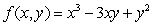 and classify each as maximum, minimum or neither.
and classify each as maximum, minimum or neither.
(Essay)
4.9/5  (32)
(32)
The monthly mortgage payment in dollars, P, for a house is a function of three variables P = f(A, r, N), where A is the amount borrowed in dollars, r is the interest rate, and N is the number of years before the mortgage is paid off. It is given that: 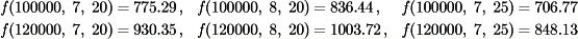 Estimate the value of
Estimate the value of 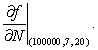
(Short Answer)
4.9/5  (43)
(43)
The following figure shows contours of 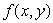 and the constraint
and the constraint 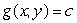 . What is the value of x that maximizes f subject to this constraint?
. What is the value of x that maximizes f subject to this constraint? 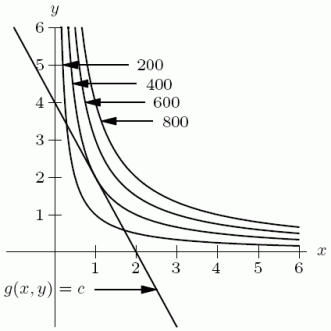
(Short Answer)
5.0/5  (40)
(40)
Suppose the Cobb-Douglas production function for a company is given by 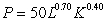 , where P is production in tons, L is the number of workers, and K is the capital investment, in thousands of dollars. How many tons are produced if the company has an initial investment of 20 thousand dollars and the company employs 16 workers? Round to the nearest ton.
, where P is production in tons, L is the number of workers, and K is the capital investment, in thousands of dollars. How many tons are produced if the company has an initial investment of 20 thousand dollars and the company employs 16 workers? Round to the nearest ton.
(Short Answer)
4.9/5  (33)
(33)
An airline's revenue, 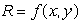 , is a function of the number of full price tickets, x, and the number of discount tickets, y, sold. When 300 full price and 600 discount tickets are sold, R = $225,000. Use partial derivatives
, is a function of the number of full price tickets, x, and the number of discount tickets, y, sold. When 300 full price and 600 discount tickets are sold, R = $225,000. Use partial derivatives 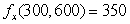 and
and 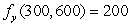 to estimate revenue when x = 304 and y = 603.
to estimate revenue when x = 304 and y = 603.
(Short Answer)
4.8/5  (30)
(30)
The following figure shows contours for the function 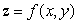 . Is z an increasing or decreasing function of x?
. Is z an increasing or decreasing function of x? 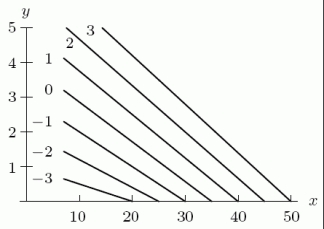
(Short Answer)
4.9/5  (33)
(33)
Showing 21 - 40 of 134
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)