Exam 8: Functions of Several Variables
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Suppose that 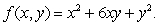 Find and classify the critical point(s) as local maxima, local minima, or neither.
Find and classify the critical point(s) as local maxima, local minima, or neither.
(Essay)
4.7/5  (27)
(27)
The volume of a cylinder is given by 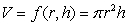 , where r is the radius of the base and h is the height, both in centimeters. At a radius of 5 centimeters and a height of 8 centimeters, how much does the volume increase for each 1 cm increase in the height?
, where r is the radius of the base and h is the height, both in centimeters. At a radius of 5 centimeters and a height of 8 centimeters, how much does the volume increase for each 1 cm increase in the height?
(Multiple Choice)
4.9/5  (28)
(28)
The number, N, of children that can be enrolled in a private school is a function of the number of certified teachers, T, and the number of aides, A, available, according to the formula 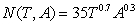 .
Teachers average an annual salary of $34,000 and aides average an annual salary of $24,000. The annual budget for salaries is B = $760,000. Using Lagrange multipliers to maximize enrollment, we find that T = _____, A = _____, and
.
Teachers average an annual salary of $34,000 and aides average an annual salary of $24,000. The annual budget for salaries is B = $760,000. Using Lagrange multipliers to maximize enrollment, we find that T = _____, A = _____, and 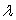 = _____. Round T and A to the nearest whole number; round
= _____. Round T and A to the nearest whole number; round 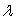 to 5 decimal places.
to 5 decimal places.
(Short Answer)
4.9/5  (35)
(35)
A certain piece of electronic surveying equipment is designed to operate in temperatures ranging from 0° C to 30° C. Its performance index, p(t, h), measured on a scale from 0 to 1, depends on both the temperature t and the humidity h of its surrounding environment. Values of the function p = f(t, h) are given in the following table. (The higher the value of p, the better the performance.) 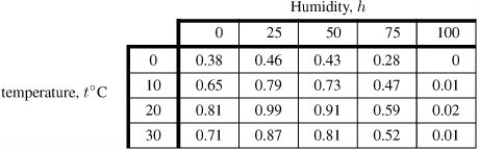 What is the value of p(20, 25)?
What is the value of p(20, 25)?
(Short Answer)
4.8/5  (21)
(21)
Consider the function 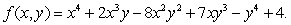 Check that (0,0) is a critical point of f and classify it as a local minimum, local maximum or neither.
Check that (0,0) is a critical point of f and classify it as a local minimum, local maximum or neither.
(Short Answer)
4.8/5  (28)
(28)
A company sells two products. The fixed costs for the company are $3300, the variable costs for the first product are $7 per unit, and the variable costs for the second product are $9 per unit.. If the company produces 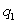 units of the first product and
units of the first product and 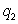 units of the second product, which of the following is a formula for the total cost, C, as a function of
units of the second product, which of the following is a formula for the total cost, C, as a function of 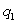 and
and 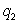 ?
?
(Multiple Choice)
4.9/5  (37)
(37)
You build a campfire while up in the mountains. It is 45 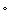 F when you start the fire. Let
F when you start the fire. Let 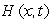 be the temperature x feet from the fire t minutes after you start it. The following figure shows the contour diagram for H. How many
be the temperature x feet from the fire t minutes after you start it. The following figure shows the contour diagram for H. How many  F is it 8 feet from the fire after 25 minutes?
F is it 8 feet from the fire after 25 minutes? 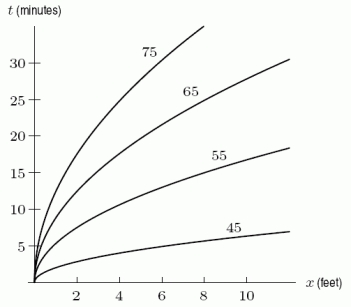
(Short Answer)
4.8/5  (39)
(39)
The consumption of beef, C (in pounds per week per household) is given by the function C = f(I, p), where I is the household income in thousands of dollars per year, and p is the price of beef in dollars per pound. Explain the meaning of the statement: 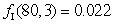 , and include units in your answer.
, and include units in your answer.
(Essay)
4.8/5  (39)
(39)
Suppose the quantity, q, of a good produced depends on the number of workers, w, and the amount of capital, k, invested and is represented by the Cobb-Douglas function 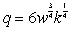 . In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $2720. Using Lagrange multipliers, find the optimum number of workers.
. In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $2720. Using Lagrange multipliers, find the optimum number of workers.
(Short Answer)
4.7/5  (36)
(36)
The ideal gas law states that 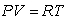 for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin) and R is a positive constant.
Find
for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin) and R is a positive constant.
Find 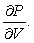
(Short Answer)
4.8/5  (38)
(38)
A table of values for 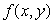 is given below. Is fx positive or negative?
is given below. Is fx positive or negative? 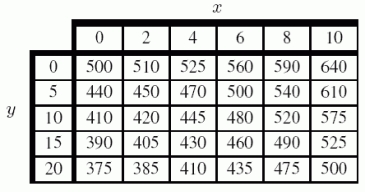
(Short Answer)
4.7/5  (24)
(24)
Find the following partial derivative: 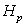 (2, 2) if
(2, 2) if 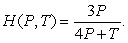 Give your answer to 4 decimal places.
Give your answer to 4 decimal places.
(Short Answer)
4.8/5  (37)
(37)
The production function for a company is 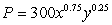 , where P is the amount produced given x units of labor and y units of equipment. Each unit of labor costs $800 and each unit of equipment costs $400. Assuming the goal of the company is to minimize cost given a fixed production goal of 9000 units produced, what is the meaning of the Lagrange multiplier
, where P is the amount produced given x units of labor and y units of equipment. Each unit of labor costs $800 and each unit of equipment costs $400. Assuming the goal of the company is to minimize cost given a fixed production goal of 9000 units produced, what is the meaning of the Lagrange multiplier 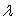 ?
?
(Multiple Choice)
4.8/5  (26)
(26)
The cost of building a new fence is 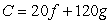 , where f is the number of linear feet of fence and g is the number of gates. Find
, where f is the number of linear feet of fence and g is the number of gates. Find 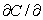 f.
f.
(Short Answer)
4.8/5  (33)
(33)
The Perfect House company produces two types of bathtub, the Hydro Deluxe model and the Singing Bird model. The company noticed that demand and prices are related. In particular,
for Hydro Deluxe: demand = 1300 - price of Hydro Deluxe + price of Singing Bird
for Singing Bird: demand = 1450 + price of Hydro Deluxe -2(price of Singing Bird).
The costs of manufacturing the Hydro Deluxe and Singing Bird are $500 and $300 per unit respectively. Determine the price of each model that gives the maximum profit.
(Short Answer)
4.8/5  (34)
(34)
The Green Leaf Bakery makes two types of chocolate cakes, Delicious and Extra Delicious. Each Delicious requires 0.1 lb of European chocolate, while each Extra Delicious requires 0.2 lb. Currently there are only 230 lb of chocolate available each month. Suppose the profit function is given by: 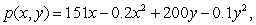 where x is the number of Delicious cakes and y is the number of Extra Delicious cakes that the bakery produces each month.
(a) How many of each cake should the bakery produce each month to maximize profit?
(b) What is the value of ? What does it mean?
(c) It will cost $36.00 to get an extra pound of European chocolate. Should the bakery buy it?
where x is the number of Delicious cakes and y is the number of Extra Delicious cakes that the bakery produces each month.
(a) How many of each cake should the bakery produce each month to maximize profit?
(b) What is the value of ? What does it mean?
(c) It will cost $36.00 to get an extra pound of European chocolate. Should the bakery buy it?
(Short Answer)
4.7/5  (44)
(44)
Plants need varying amount of water and sunlight to grow. The following contour diagrams each show the growth of a different plant as a function of the amount of water and sunlight. Which diagram would represent a plant that does best in a temperate climate (moderate water and sunshine)? 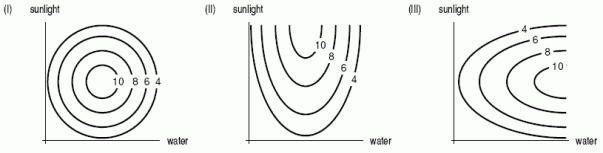
(Short Answer)
5.0/5  (40)
(40)
A company manufactures x units of one item and y units of another. The total cost, C, in dollars of producing these two items is given by the function 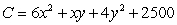 .
Use Lagrange multipliers to find the minimum cost subject to the constraint that 100 items (total) must be produced. The minimum cost occurs when x = _____ and y = _____. Round your answers to the nearest whole number.
.
Use Lagrange multipliers to find the minimum cost subject to the constraint that 100 items (total) must be produced. The minimum cost occurs when x = _____ and y = _____. Round your answers to the nearest whole number.
(Short Answer)
4.7/5  (32)
(32)
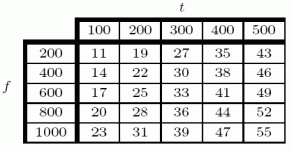
The following table shows the revenue R, (in hundreds of dollars) at a movie theater as a function of the number of tickets sold, t, and the number of food items sold, f. Thus, 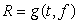 . Find
. Find 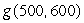 .
. 
(Short Answer)
4.7/5  (31)
(31)
Showing 81 - 100 of 134
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)