Exam 8: Functions of Several Variables
Exam 1: Functions and Change204 Questions
Exam 2: Rate of Change: the Derivative132 Questions
Exam 3: Shortcuts to Differentiation178 Questions
Exam 4: Using the Derivative94 Questions
Exam 5: Accumulated Change: the Definite Integral93 Questions
Exam 6: Antiderivatives and Applications122 Questions
Exam 7: Probability68 Questions
Exam 8: Functions of Several Variables134 Questions
Exam 9: Mathematical Modeling Using Differential Equations121 Questions
Exam 10: Geometric Series65 Questions
Select questions type
Find all the critical points of the function 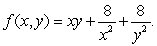 Classify these critical points as local maxima, local minima, or neither.
Classify these critical points as local maxima, local minima, or neither.
(Short Answer)
4.9/5  (33)
(33)
A company manufactures x units of one item and y units of another. The total cost, C, in dollars of producing these two items is given by the function 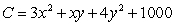 .
Use Lagrange multipliers to find the minimum cost subject to the constraint that 100 items (total) must be produced. What is the value of
.
Use Lagrange multipliers to find the minimum cost subject to the constraint that 100 items (total) must be produced. What is the value of 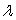 to one decimal place?
to one decimal place?
(Short Answer)
4.8/5  (36)
(36)
You build a campfire while up in the mountains. It is 45  F when you start the fire. Let
F when you start the fire. Let 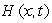 be the temperature x feet from the fire t minutes after you start it. The following figure shows the contour diagram for H. Is H an increasing or decreasing function of x?
be the temperature x feet from the fire t minutes after you start it. The following figure shows the contour diagram for H. Is H an increasing or decreasing function of x? 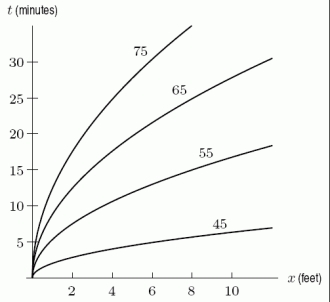
(Short Answer)
4.7/5  (36)
(36)
A mop company can produce 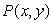 mops using x units of capital and y units of labor, with production costs
mops using x units of capital and y units of labor, with production costs 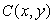 dollars. With a budget of $400,000, the maximum production is 65,000, using $300,000 in capital and $100,000 in labor. The Lagrange multiplier is
dollars. With a budget of $400,000, the maximum production is 65,000, using $300,000 in capital and $100,000 in labor. The Lagrange multiplier is 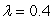 . What are the units for
. What are the units for 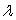 ?
?
(Multiple Choice)
4.8/5  (35)
(35)
The monthly mortgage payment in dollars, P, for a house is a function of three variables P = f(A, r, N), where A is the amount borrowed in dollars, r is the interest rate, and N is the number of years before the mortgage is paid off. It is given that:
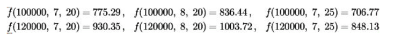 Estimate the value of
Estimate the value of 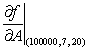 and interpret your answer in terms of a mortgage payment. Select all answers that apply.
and interpret your answer in terms of a mortgage payment. Select all answers that apply.
(Multiple Choice)
4.9/5  (39)
(39)
Which of the following describes the contour diagram for the function 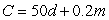 (with m on the vertical axis and d on the horizontal axis)?
(with m on the vertical axis and d on the horizontal axis)?
(Multiple Choice)
4.8/5  (28)
(28)
A company sells two products. The fixed costs for the company are $2500, the variable costs for the first product are $5 per unit, and the variable costs for the second product are $9 per unit.. If the company produces 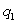 units of the first product and
units of the first product and 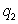 units of the second product, and the total cost is given by
units of the second product, and the total cost is given by 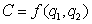 , what is
, what is 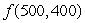 ?
?
(Short Answer)
4.8/5  (36)
(36)
Estimate fy (3,2) from the contour diagram shown below. Use the next higher point to make your estimate. 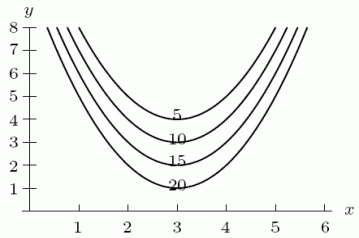
(Short Answer)
4.9/5  (37)
(37)
The amount, 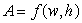 , of your paycheck is a function of your hourly wage, w, and the number of hours, h, you work. What does the statement
, of your paycheck is a function of your hourly wage, w, and the number of hours, h, you work. What does the statement 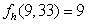 mean in terms of your paycheck?
mean in terms of your paycheck?
(Multiple Choice)
4.8/5  (34)
(34)
Use Lagrange multipliers to find the maximum and minimum values of 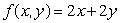 , subject to the constraint
, subject to the constraint 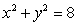 . For the minimum value,
. For the minimum value, 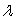 = _____ (use the decimal form), and the minimum value of
= _____ (use the decimal form), and the minimum value of 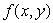 is _____.
is _____.
(Short Answer)
4.7/5  (31)
(31)
The function 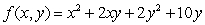 has a local __________ (maximum / minimum / neither) at the critical point, where x = _____ and y = _____.
has a local __________ (maximum / minimum / neither) at the critical point, where x = _____ and y = _____.
(Short Answer)
4.9/5  (34)
(34)
The monthly car payment for a new car is a function of three variables, 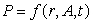 , where r is the annual interest rate, A is the amount borrowed in dollars, and t is time in months before the car is paid off. Would you expect fA
, where r is the annual interest rate, A is the amount borrowed in dollars, and t is time in months before the car is paid off. Would you expect fA
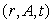 to be increasing or decreasing?
to be increasing or decreasing?
(Short Answer)
4.9/5  (33)
(33)
The function 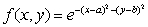 where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points. Show that f(x, y) has a maximum at (a, b).
where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points. Show that f(x, y) has a maximum at (a, b).
(Essay)
4.9/5  (37)
(37)
Find the maximum value of 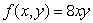 subject to the constraint equation
subject to the constraint equation 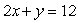 using Lagrange multipliers.
using Lagrange multipliers.
(Short Answer)
4.8/5  (38)
(38)
Suppose that you want to find the maximum and minimum values of 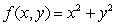 subject to the constraint x + 6y = 4.
Use the method of Lagrange multipliers to find the exact location(s) of any extrema.
subject to the constraint x + 6y = 4.
Use the method of Lagrange multipliers to find the exact location(s) of any extrema.
(Short Answer)
4.8/5  (37)
(37)
Yummy Potato Chip Company has manufacturing plants in N.Y. and N.J. The cost of manufacturing depends on the quantities (in thousand of bags), q1 and q2, produced in the N.Y. and N.J. factories respectively. Suppose the cost function is given by 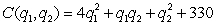 Find
Find 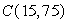 .
.
(Short Answer)
4.8/5  (33)
(33)
The quantity, Q, of a good produced depends on the quantities 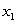 and
and 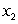 of the two main materials used:
of the two main materials used: 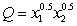 . Material
. Material 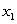 costs $75 per unit, and material
costs $75 per unit, and material 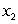 costs $25 per unit. We want to minimize the cost of producing 100 units of the good. What is the constraint function?
costs $25 per unit. We want to minimize the cost of producing 100 units of the good. What is the constraint function?
(Multiple Choice)
4.9/5  (31)
(31)
Showing 41 - 60 of 134
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)