Exam 7: Applications of Integration
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find the area of the region bounded by the graphs of the algebraic functions. 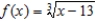
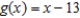
(Multiple Choice)
4.9/5  (46)
(46)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the x-axis. 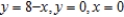
(Multiple Choice)
4.8/5  (34)
(34)
A force of 25 pounds stretches a spring 11 inches in an exercise machine. Find the work done in stretching the spring 3 feet from its natural position.
(Multiple Choice)
4.8/5  (31)
(31)
Use the disk or the shell method to find the volume of the solid generated by revolving the region bounded by the graphs of the equations 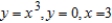 about the line
about the line 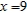 .
.
(Multiple Choice)
4.8/5  (40)
(40)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region bounded by 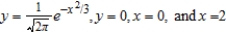 about the y-axis. Round your answer to three decimal places.
about the y-axis. Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (35)
(35)
Find the area of the region bounded by the graphs of the equations. 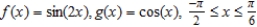 .
.
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the 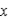 -axis. Verify your results using the integration capabilities of a graphing utility.
-axis. Verify your results using the integration capabilities of a graphing utility. 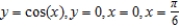
(Multiple Choice)
4.9/5  (33)
(33)
A tank with a base of 4 feet by 5 feet and a height of 4 feet is full of water. The water weighs 62.4 pounds per cubic foot. How much work is done in pumping water out over the top edge in order to empty all of the tank. Round your answer to one decimal place. 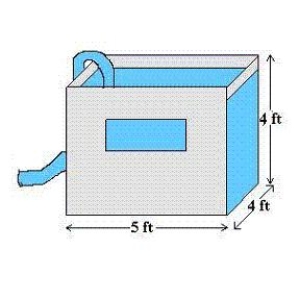
(Multiple Choice)
4.8/5  (33)
(33)
A solid is generated by revolving the region bounded by 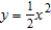 and
and 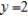 about the y-axis. A hole, centered along the axis of revolution, is drilled through this solid so that one-fourth of the volume is removed. Find the diameter of the hole. Round your answer to three decimal places.
about the y-axis. A hole, centered along the axis of revolution, is drilled through this solid so that one-fourth of the volume is removed. Find the diameter of the hole. Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
The figure is the vertical side of a form for poured concrete that weighs 140.7 pounds per cubic foot. Dimensions in the figure are in feet. Determine force on this part of the concrete form. 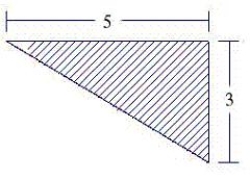
(Multiple Choice)
4.8/5  (41)
(41)
The surface of a machine part is the region between the graphs of 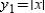 and
and 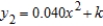 as shown in the figure. Find k if the parabola is tangent to the graph of y1. Round your answer to three decimal places.
as shown in the figure. Find k if the parabola is tangent to the graph of y1. Round your answer to three decimal places. 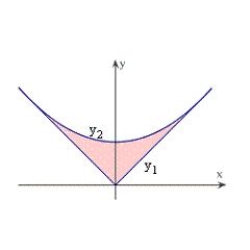
(Multiple Choice)
4.8/5  (33)
(33)
A quantity of a gas with an initial volume of 2 cubic feet and a pressure of 4500 pounds per square foot expands to a volume of 7 cubic feet. Find the work done by the gas. Round your answer to two decimal places. Assume the temperature of the gas in this process remain constant.
(Multiple Choice)
5.0/5  (34)
(34)
Find Mx, My, and 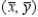 for the lamina of uniform density ρ bounded by the graphs of the equations
for the lamina of uniform density ρ bounded by the graphs of the equations 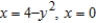 .
.
(Multiple Choice)
4.8/5  (42)
(42)
Neglecting air resistance and the weight of the propellant, determine the work done in propelling a 10-ton satellite to a height of 200 miles above Earth. Assume that the Earth has a radius of 4000 miles.
(Multiple Choice)
4.8/5  (32)
(32)
Find the arc length from 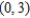 clockwise to
clockwise to 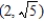 along the circle
along the circle 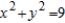 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (27)
(27)
Find the arc length of the graph of the function ![Find the arc length of the graph of the function over the interval [1,2].](https://storage.examlex.com/TB8527/11eb71ff_b3aa_65b0_8413_457b87d41b08_TB8527_11.jpg) over the interval [1,2].
over the interval [1,2].
(Multiple Choice)
4.8/5  (28)
(28)
Find the arc length of the graph of the function ![Find the arc length of the graph of the function over the interval [0,5].](https://storage.examlex.com/TB8527/11eb71ff_b3ad_7353_8413_6b3e39ffee74_TB8527_11.jpg) over the interval [0,5].
over the interval [0,5].
(Multiple Choice)
4.9/5  (45)
(45)
The area of the top side of a piece of sheet metal is 10 square feet. The sheet metal is submerged horizontally in 6 feet of water. Find the fluid force on the top side. Round your answer to one decimal place.
(Multiple Choice)
4.9/5  (31)
(31)
Use the shell method to set up and evaluate the integral that gives the volume of the solid generated by revolving the plane region about the x-axis. 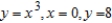
(Multiple Choice)
4.9/5  (36)
(36)
A cylindrical water tank 5 meters high with a radius of 3 meters is buried so that the top of the tank is 1 meter below ground level. How much work is done in pumping a full tank of water up to ground level? (The water weighs 9800 newtons per cubic meter.)
(Multiple Choice)
4.8/5  (30)
(30)
Showing 81 - 100 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)