Exam 6: Differential Equations
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find an equation of the graph that passes through the point 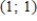 and has the slope
and has the slope 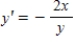 .
.
(Multiple Choice)
4.8/5  (37)
(37)
Suppose that the population (in millions) of a Uganda in 2007 is 30.3 and that expected continuous annual rate of change of the population is 0.036. The exponential growth model for the population by letting 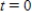 corresponds to 2000 is
corresponds to 2000 is 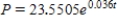 . Use the model to predict the population of the country in 2014. Round your answer to two decimal places.
. Use the model to predict the population of the country in 2014. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Sketch the slope field for the differential equation 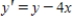 and use the slope field to sketch the solution that passes through the point
and use the slope field to sketch the solution that passes through the point 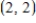 .
.
(Multiple Choice)
4.8/5  (46)
(46)
The logistic function 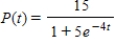 models the growth of a population. Determine when the population reaches
models the growth of a population. Determine when the population reaches 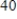 % of the maximum carrying capacity. Round your answer to three decimal places.
% of the maximum carrying capacity. Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (37)
(37)
Suppose that the population (in millions) of Hungary in 2007 was 10 and that the expected continuous annual rate of change of the population is -0.003. Find the exponential growth model 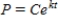 for the population by letting
for the population by letting 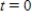 correspond to 2000. Round your answer to four decimal places.
correspond to 2000. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
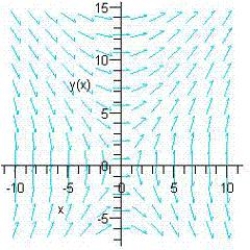
Use the differential equation 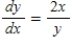 and its slope field to find the slope at the point
and its slope field to find the slope at the point 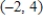 .
. 
(Multiple Choice)
4.7/5  (36)
(36)
The isotope 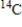 has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 2.1 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18,000 years)? Round your answers to four decimal places.
has a half-life of 5,715 years. After 2,000 years, a sample of the isotope is reduced to 2.1 grams. What was the initial size of the sample (in grams)? How much will remain after 20,000 years (i.e., after another 18,000 years)? Round your answers to four decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
A phase trajectory is shown for populations of rabbits and foxes. Describe how each population changes as time goes by. 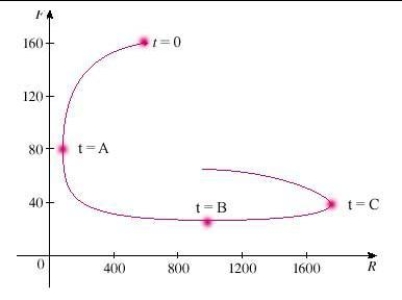
Select the correct statement.
Select the correct statement.
(Multiple Choice)
4.8/5  (36)
(36)
Use integration to find a general solution of the differential equation . 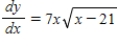
(Multiple Choice)
4.9/5  (33)
(33)
A conservation organization releases 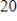
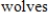 into a preserve. After
into a preserve. After  years, there are
years, there are 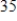
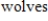 in the preserve. The preserve has a carrying capacity of
in the preserve. The preserve has a carrying capacity of 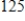 . Write a logistic function that models the population of
. Write a logistic function that models the population of  in the preserve.
in the preserve.
(Multiple Choice)
4.8/5  (42)
(42)
Find an equation of the graph that passes through the point 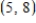 and has the slope
and has the slope 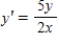 .
.
(Multiple Choice)
4.7/5  (43)
(43)
Use integration to find a general solution of the differential equation. 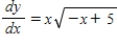
(Multiple Choice)
4.8/5  (34)
(34)
Use 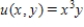 as a integrating factor to find the general solution of the differential equation
as a integrating factor to find the general solution of the differential equation 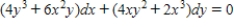 .
.
(Multiple Choice)
4.8/5  (39)
(39)
A 500-gallon tank is half full of distilled water. At time 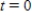 , a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 11 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 9 gallons per minute. At what time will the tank be full?
, a solution containing 0.5 pound of concentrate per gallon enters the tank at the rate of 11 gallons per minute, and the well-stirred mixture is withdrawn at the rate of 9 gallons per minute. At what time will the tank be full?
(Multiple Choice)
4.8/5  (43)
(43)
Each of the following graphs is from a logistic function 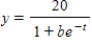 . Which one has the largest value of b?
. Which one has the largest value of b?
(Multiple Choice)
4.8/5  (35)
(35)
The logistic function 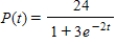 models the growth of a population. Identify the initial population.
models the growth of a population. Identify the initial population.
(Multiple Choice)
4.9/5  (33)
(33)
Showing 41 - 60 of 93
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)