Exam 13: Functions of Several Variables
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
The material for constructing the base of an open box costs 1.5 times as much per unit area as the material for constructing the sides. For a fixed amount of money $400.00, find the dimensions of the box of largest volume that can be made.
(Multiple Choice)
4.9/5  (30)
(30)
Examine the function 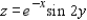 for relative extrema and saddle points.
for relative extrema and saddle points. 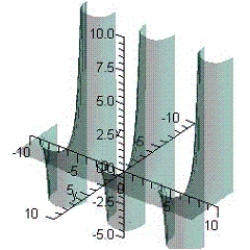
(Multiple Choice)
4.9/5  (31)
(31)
Use Lagrange multipliers to minimize the function 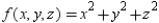 subject to the following constraint.
subject to the following constraint. 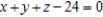
Assume that x, y, and z are positive.
Assume that x, y, and z are positive.
(Multiple Choice)
4.7/5  (36)
(36)
Find the directional derivative of the function 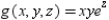 at
at 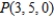 in the direction of
in the direction of 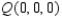 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (38)
(38)
The temperature at the point 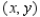 on a metal plate is modeled by
on a metal plate is modeled by 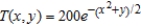 ,
, 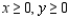 . Find the directions of no change in heat on the plate from the point
. Find the directions of no change in heat on the plate from the point 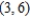 .
.
(Multiple Choice)
4.7/5  (34)
(34)
Use Lagrange multipliers to minimize the function 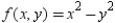 subject to the following constraint:
subject to the following constraint: 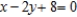
Assume that x and y are positive.
Assume that x and y are positive.
(Multiple Choice)
4.9/5  (33)
(33)
The surface of a mountain is modeled by the equation 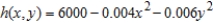 . A mountain climber is at the point
. A mountain climber is at the point 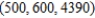 . In what direction should the climber move in order to ascend at the greatest rate? Round all numerical values in your answer to one decimal place.
. In what direction should the climber move in order to ascend at the greatest rate? Round all numerical values in your answer to one decimal place.
(Multiple Choice)
4.8/5  (29)
(29)
Suppose the period T of a pendulum of length L is 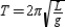 where g is the acceleration due to gravity. A pendulum is moved from the Canal Zone, where
where g is the acceleration due to gravity. A pendulum is moved from the Canal Zone, where 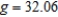 feet per second per second, to Greenland, where
feet per second per second, to Greenland, where 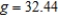 feet per second per second. Because of the change in temperature, the length of the pendulum changes from 2.5 feet to 2.43 feet. Approximate the change in the period of the pendulum. Round your answer to four decimal places.
feet per second per second. Because of the change in temperature, the length of the pendulum changes from 2.5 feet to 2.43 feet. Approximate the change in the period of the pendulum. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
Find the absolute extrema of the function 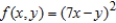 over the triangular region in the xy-plane with vertices
over the triangular region in the xy-plane with vertices 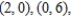 and
and 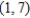 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Examine the function 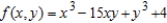 for relative extrema and saddle points.
for relative extrema and saddle points.
(Multiple Choice)
4.8/5  (41)
(41)
Find 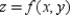 and use the total differential to approximate the quantity
and use the total differential to approximate the quantity 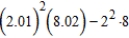 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 101 - 120 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)