Exam 13: Functions of Several Variables
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find the point(s) on the hyperboloid 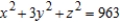 where the tangent plane is perpendicular to the line with parametric equations
where the tangent plane is perpendicular to the line with parametric equations 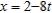 ,
, 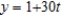 and
and 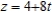 .
.
(Multiple Choice)
4.7/5  (31)
(31)
Given 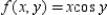 , use the total differential to approximate
, use the total differential to approximate 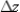 at
at 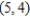 towards
towards 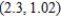 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (34)
(34)
Suppose a home improvement contractor is painting the walls and ceiling of a rectangular room. The volume of the room is 911.25 cubic feet. The cost of wall paint is $0.08 per square foot and the cost of ceiling paint is $0.19 per square foot. Let x, y, and z be the length, width, and height of a rectangular room respectively. Find the room dimensions that result in a minimum cost for the paint. Round your answers to two decimal places.
(Multiple Choice)
4.8/5  (34)
(34)
Find the least squares regression line for the points 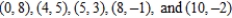 . Round numerical values in your answer to two decimal places.
. Round numerical values in your answer to two decimal places.
(Multiple Choice)
4.7/5  (31)
(31)
Find 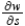 using the appropriate Chain Rule for
using the appropriate Chain Rule for 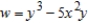 where
where 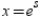 and
and 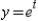 , and evaluate the partial derivative at
, and evaluate the partial derivative at 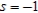 and
and 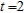 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (24)
(24)
Find 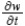 using the appropriate Chain Rule for
using the appropriate Chain Rule for 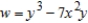 where
where 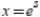 and
and 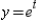 , and evaluate the partial derivative at
, and evaluate the partial derivative at 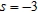 and
and 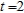 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (25)
(25)
Use Lagrange multipliers to find the minimum distance from the line 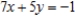 to the point
to the point 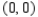 .
.
(Multiple Choice)
4.9/5  (42)
(42)
Suppose a trough with trapezoidal cross sections is formed by turning up the edges of a 30-inch-wide sheet of aluminum (see figure). Find the cross section of maximum area. 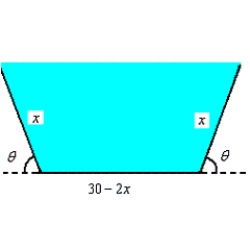
(Multiple Choice)
4.9/5  (43)
(43)
Given 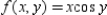 , calculate
, calculate 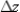 by evaluating
by evaluating 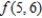 and
and 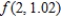 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Use Lagrange multipliers to find the minimum distance from the circle 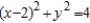 to the point
to the point 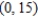 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Find an equation of the tangent plane to the surface 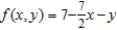 at the point
at the point 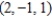 .
.
(Multiple Choice)
5.0/5  (33)
(33)
A company manufactures two types of sneakers: running shoes and basketball shoes. The total revenue from 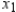 units of running shoes and
units of running shoes and 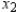 units of basketball shoes is:
units of basketball shoes is: 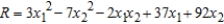 ,
Where
,
Where 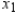 and
and 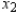 are in thousands of units. Find
are in thousands of units. Find 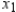 and
and 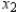 so as to maximize the revenue.
so as to maximize the revenue.
(Multiple Choice)
4.8/5  (24)
(24)
Showing 141 - 160 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)