Exam 13: Functions of Several Variables
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Use Lagrange multipliers to maximize the function 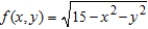 subject to the following constraint.
subject to the following constraint. 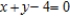 Assume that x and y are positive.
Assume that x and y are positive.
(Multiple Choice)
4.8/5  (47)
(47)
Suppose the centripetal acceleration of a particle moving in a circle is 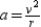 , where v is the velocity and r is the radius of the circle. Approximate the maximum percent error in measuring the acceleration due to errors of 7% in v and 5% in r.
, where v is the velocity and r is the radius of the circle. Approximate the maximum percent error in measuring the acceleration due to errors of 7% in v and 5% in r.
(Multiple Choice)
4.8/5  (32)
(32)
The two radii of the frustum of a right circular cone are increasing at a rate of 5 centimeters per minute, and the height is increasing at a rate of 12 centimeters per minute (see figure). Find the rate at which the volume is changing when the two radii are 18 centimeters and 30 centimeters, and the height is 14 centimeters. 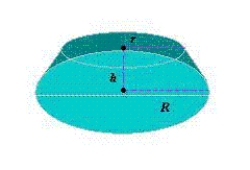
(Multiple Choice)
4.7/5  (33)
(33)
A rectangular box with an open top has a length of x feet, a width of y feet, and a height of z feet. It costs $1.80 per square foot to build the base and $0.45 per square foot to build the sides. Write the cost C of constructing the box as a function of x, y, and z.
(Multiple Choice)
4.8/5  (31)
(31)
Find the angle of inclination 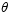 of the tangent plane to the surface
of the tangent plane to the surface 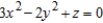 at the point
at the point 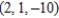 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
Find the least squares regression line for the points shown in the graph. 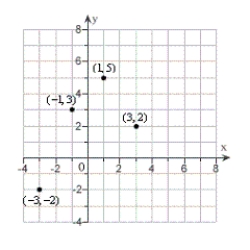
(Multiple Choice)
4.8/5  (33)
(33)
Find the path of a heat-seeking particle placed at point 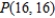 on a metal plate with a temperature field
on a metal plate with a temperature field 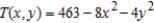 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Find symmetric equations of the normal line to the surface 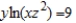 at the point
at the point 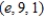 .
.
(Multiple Choice)
4.9/5  (25)
(25)
Determine the continuity of the composite function 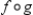 where
where 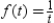 and
and 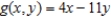 .
.
(Multiple Choice)
4.8/5  (46)
(46)
Find the highest point on the curve of intersection of the following surfaces. Cone: 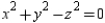 , Plane:
, Plane: 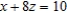
(Multiple Choice)
4.8/5  (41)
(41)
Given 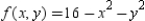 , calculate
, calculate 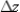 by evaluating
by evaluating 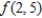 and
and 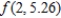 . Round your answer to four decimal places.
. Round your answer to four decimal places.
(Multiple Choice)
4.8/5  (30)
(30)
Assume a rule that is one of several methods used to determine the lumber yield of a log (in board-feet) in terms of its diameter d (in inches) and its length L (in feet). The number of board-feet is 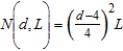 . Find the number of board-feet of lumber in a log 46 inches in diameter and 20 feet in length.
. Find the number of board-feet of lumber in a log 46 inches in diameter and 20 feet in length.
(Multiple Choice)
4.8/5  (32)
(32)
Find the absolute extrema of 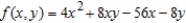 on the region bounded by the square with vertices
on the region bounded by the square with vertices 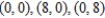 and
and 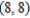 .
.
(Multiple Choice)
4.9/5  (26)
(26)
Use Lagrange multipliers to find the maximum value of 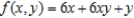 where
where 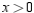 and
and 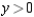 subject to the constraint
subject to the constraint 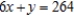 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Use the gradient to find a normal vector to the graph of the equation at the given point. 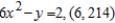
(Multiple Choice)
4.7/5  (37)
(37)
Showing 121 - 140 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)