Exam 4: Consumer Behavior
Exam 1: Adventures in Microeconomics20 Questions
Exam 2: Supply and Demand148 Questions
Exam 3: Using Supply and Demand to Analyze Markets146 Questions
Exam 4: Consumer Behavior130 Questions
Exam 5: Individual and Market Demand146 Questions
Exam 6: Producer Behavior142 Questions
Exam 7: Costs179 Questions
Exam 8: Supply in a Competitive Market148 Questions
Exam 9: Market Power and Monopoly162 Questions
Exam 10: Market Power and Pricing Strategies165 Questions
Exam 11: Imperfect Competition172 Questions
Exam 12: Game Theory170 Questions
Exam 13: Factor Markets94 Questions
Exam 14: Investment, Time, and Insurance117 Questions
Exam 15: General Equilibrium97 Questions
Exam 16: Asymmetric Information106 Questions
Exam 17: Externalities and Public Goods114 Questions
Exam 18: Behavioral and Experimental Economics112 Questions
Select questions type
Cashews are sold in either 8-ounce (C8) or 16-ounce (C16) cans.
a. Write an equation that represents a person's utility function for C8 and C16.
b. What is the MRS? (Assume that 16-ounce cans are measured on the y-axis and 8-ounce cans are measured on the x-axis.)
(Essay)
4.8/5  (36)
(36)
The consumer's budget constraint is $6 = 0.50G + P, where G is packs of gum and P is bags of pretzels. The marginal utility of pretzels is MUP = G0.5, and the marginal utility of gum is MUG = 0.5G-0.5P. The consumer's utility function is U = G0.5P. The utility-maximizing bundle consists of _____ packs of gum and _____ bags of pretzels.
(Multiple Choice)
4.8/5  (33)
(33)
Suppose that Lloyd cares only about shoes and clothes. Lloyd's utility function is U = S0.5C0.5, where S is the number of pairs of shoes and C is the number of clothing items that Lloyd owns. The price of shoes is $80, and the price of clothes is $100. Lloyd has a budget of $3200. Which levels of S and C maximize Lloyd's utility?
(Multiple Choice)
4.9/5  (37)
(37)
A consumer buys coffee (C) for $3 each and bagels (B) for $1.50 each. She has income of $40. If the coffee shop limits the number of bagels that a customer may purchase to 6, what is the equation of her budget constraint?
(Essay)
4.8/5  (36)
(36)
Parker consumes goods X and Y. Her utility function is U = XY, which means that MUX = Y and MUY = X. Prove that Parker's utility function satisfies all four assumptions of consumer preferences.
(Essay)
4.9/5  (34)
(34)
Pedro loves leather belts but neither likes nor dislikes additional silk ties. Draw Pedro's indifference curve, using a well-labeled diagram.
(Essay)
4.8/5  (27)
(27)
Esther has an income of $80, and she consumes pizza (P) and soda (S). The price of pizza is $10, and the price of soda is $4.
a. Graph Esther's budget constraint.
b. Graph Esther's budget constraint assuming that there is a buy-one-get-one-free pizza special.
c. Graph Esther's budget constraint assuming that there is a buy-two-get-one-free pizza special.
(Essay)
4.7/5  (32)
(32)
(Figure: Concert Tickets and Movie Tickets I) Use the graph to answer the following questions. 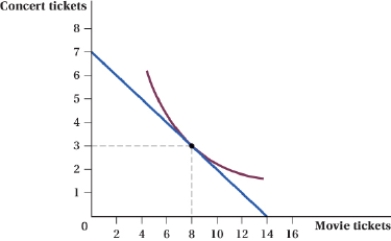 a. What is the marginal rate of substitution at 3 concert tickets and 8 movie tickets?
b. If the consumer's income decreases by 10% and the price of both goods decreases by 10%, how many concert and movie tickets will the consumer purchase?
c. If the price of movie tickets doubles, what does the marginal rate of substitution equal at the new utility-maximizing point?
a. What is the marginal rate of substitution at 3 concert tickets and 8 movie tickets?
b. If the consumer's income decreases by 10% and the price of both goods decreases by 10%, how many concert and movie tickets will the consumer purchase?
c. If the price of movie tickets doubles, what does the marginal rate of substitution equal at the new utility-maximizing point?
(Essay)
4.8/5  (38)
(38)
If a consumer's budget constraint has a slope that is less than -1:
(Multiple Choice)
4.9/5  (34)
(34)
Mika spends all of her income on pizza and gasoline. Suppose Mika is presented with two options: A and B. Option A will subsidize gasoline by decreasing its price by 50%. Option B will increase Mika's income by the cost of the subsidy in Option A. Which of the following must be true?
(Multiple Choice)
4.8/5  (31)
(31)
Yanas ratio of marginal utility for coffee and soda is 3:1, while the price ratio of coffee to soda is 1.5:1. Which of the following statements is (are) TRUE?
I. Coffee provides Yana with 3 times the marginal utility of soda.
II. Yana could increase utility by decreasing her consumption of coffee by 3 units and increasing her consumption of soda by 1.5 units.
III. Yana could increase utility by decreasing her consumption of soda by 3 units and increasing her consumption of coffee by 2 units.
IV. Yana could increase utility by decreasing her consumption of coffee by 1 unit and increasing her consumption of soda by 3 units.
(Multiple Choice)
4.9/5  (34)
(34)
Suppose that the marginal utility of good X and good Y is given by the following equations:
MUX = 1/(X + 10)
MUY = 1/Y
a. As more units of good X are consumed, what happens to utility and marginal utility of good X?
b. What is the value of MRSXY?
(Essay)
4.8/5  (30)
(30)
Suppose that MUY = 15, MUX = 10, PY = $2, and PX = $1. Which of the following statements is TRUE?
(Multiple Choice)
4.7/5  (39)
(39)
Suppose that Maria cares only about shoes and clothes. Her utility function is U = S0.5C0.5, where S is the number of pairs of shoes and C is the number of clothing items that she owns. The price of shoes is $80, and the price of clothes is $100. Suppose that Maria must have 1,000 units of utility and wants to achieve this level of utility with the lowest possible expenditure. How can Maria's expenditure minimization problem be expressed as a Lagrangian equation?
(Multiple Choice)
4.9/5  (33)
(33)
The equation for the marginal rate of substitution of good X for good Y (that is, MRSXY) is given by:
(Multiple Choice)
4.8/5  (29)
(29)
(Figure: Video Games and Guitars I) _____ is willing to give up a lot guitars for a small number of video games, and _____ is willing to give up a lot of video games for a small number of guitars. 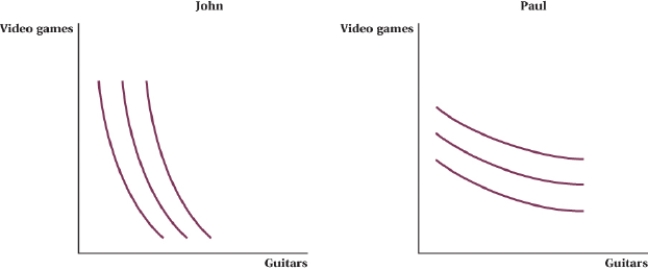
(Multiple Choice)
4.7/5  (28)
(28)
(Figure: Good Y and Good X III) The indifference curve _____ indicates that the two goods, X and Y, are relatively poor substitutes for one another, whereas the indifference curve _____ indicates that the two goods are close substitutes for one another. 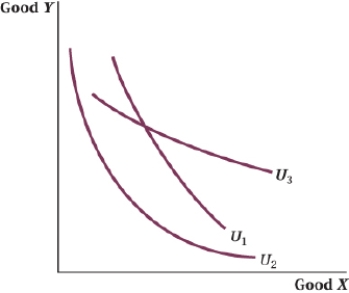
(Multiple Choice)
4.8/5  (33)
(33)
Suppose that U = min{2X, Y}, where X is units of good X and Y is units of good Y. The price of good X is $4, and the price of good Y is $7. What is the minimum expenditure necessary to achieve a utility level of 100?
(Essay)
4.9/5  (37)
(37)
Ines considers Titleist (T) and Callaway (C) golf balls perfect substitutes. Her utility function is U = 10T + 8C. A sleeve of Titleist is priced at $12, compared to $10 for Callaway balls. What is Ines's utility-maximizing bundle of golf balls? Assume that Ines can spend $120.
(Essay)
4.8/5  (41)
(41)
Manu wants to achieve a utility level of 100. His utility function is U = XY, where MUX = Y and MUY = X. What is the least amount of money (M) that Manu can spend to achieve a utility level of 100? Manu's budget constraint is M = 8X + 2Y.
(Essay)
4.8/5  (29)
(29)
Showing 41 - 60 of 130
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)