Exam 12: Multiple Integrals
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Evaluate the integral 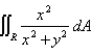 , where R is the annular region bounded by the circles
, where R is the annular region bounded by the circles 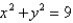 and
and 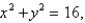 by changing to polar coordinates.
by changing to polar coordinates.
(Short Answer)
4.9/5  (35)
(35)
Express the integral as an iterated integral of the form 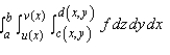 where E is the solid bounded by the surfaces
where E is the solid bounded by the surfaces 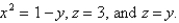
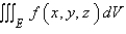
(Short Answer)
4.8/5  (33)
(33)
Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length 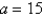 if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse. Assume the vertex opposite the hypotenuse is located at
if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse. Assume the vertex opposite the hypotenuse is located at 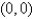 , and that the sides are along the positive axes.
, and that the sides are along the positive axes.
(Multiple Choice)
4.9/5  (30)
(30)
Estimate the volume of the solid that lies above the square 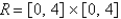 and below the elliptic paraboloid
and below the elliptic paraboloid 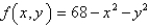 .Divide
.Divide 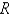 into four equal squares and use the Midpoint rule.
into four equal squares and use the Midpoint rule.
(Multiple Choice)
4.9/5  (30)
(30)
Evaluate the iterated integral 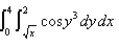 by reversing the order of integration.
by reversing the order of integration.
(Short Answer)
4.9/5  (36)
(36)
A swimming pool is circular with a 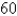 -ft diameter. The depth is constant along east-west lines and increases linearly from
-ft diameter. The depth is constant along east-west lines and increases linearly from 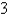 ft at the south end to
ft at the south end to 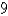 ft at the north end. Find the volume of water in the pool.
ft at the north end. Find the volume of water in the pool.
(Multiple Choice)
4.7/5  (30)
(30)
An agricultural sprinkler distributes water in a circular pattern of radius 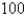 ft. It supplies water to a depth of
ft. It supplies water to a depth of 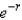 feet per hour at a distance of
feet per hour at a distance of 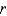 feet from the sprinkler. What is the total amount of water supplied per hour to the region inside the circle of radius
feet from the sprinkler. What is the total amount of water supplied per hour to the region inside the circle of radius 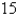 feet centered at the sprinkler?
feet centered at the sprinkler?
(Short Answer)
4.8/5  (29)
(29)
Use cylindrical coordinates to evaluate the triple integral 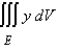 where E is the solid that lies between the cylinders
where E is the solid that lies between the cylinders 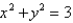 and
and 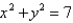 above the xy-plane and below the plane
above the xy-plane and below the plane 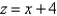 .
.
(Multiple Choice)
4.7/5  (39)
(39)
Find the moment of inertia about the y-axis for a cube of constant density 3 and side length 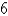 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.
(Short Answer)
4.8/5  (38)
(38)
Calculate the double integral. Round your answer to two decimal places. 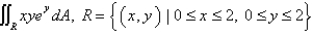
(Short Answer)
4.8/5  (29)
(29)
Find the mass of the lamina that occupies the region 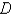 and has the given density function. Round your answer to two decimal places.
and has the given density function. Round your answer to two decimal places. 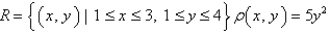
(Short Answer)
4.8/5  (40)
(40)
Use a double integral to find the area of the region R where R is bounded by the circle 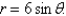
(Multiple Choice)
4.8/5  (25)
(25)
Use polar coordinates to find the volume of the solid under the paraboloid 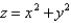 and above the disk
and above the disk 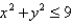 .
.
(Multiple Choice)
4.9/5  (41)
(41)
Showing 41 - 59 of 59
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)