Exam 12: Multiple Integrals
Exam 1: Functions and Limits54 Questions
Exam 2: Derivatives50 Questions
Exam 3: Inverse Functions: Exponential, Logarithmic, and Inverse Trigonometric Functions43 Questions
Exam 4: Applications of Differentiation68 Questions
Exam 5: Integrals33 Questions
Exam 6: Techniques of Integration46 Questions
Exam 7: Applications of Integration69 Questions
Exam 8: Series51 Questions
Exam 9: Parametric Equations and Polar Coordinates30 Questions
Exam 10: Vectors and the Geometry of Space68 Questions
Exam 11: Partial Derivatives73 Questions
Exam 12: Multiple Integrals59 Questions
Exam 13: Vector Calculus54 Questions
Select questions type
Use the given transformation to evaluate the integral. 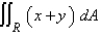 , where R is the square with vertices (0, 0), (4, 6), (6,
, where R is the square with vertices (0, 0), (4, 6), (6, 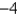 ), (10, 2) and
), (10, 2) and 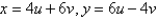
(Multiple Choice)
4.7/5  (30)
(30)
Use spherical coordinates to find the moment of inertia of the solid homogeneous hemisphere of radius 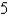 and density 1 about a diameter of its base.
and density 1 about a diameter of its base.
(Multiple Choice)
4.8/5  (41)
(41)
Use polar coordinates to find the volume of the sphere of radius 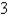 . Round to two decimal places.
. Round to two decimal places.
(Multiple Choice)
4.8/5  (40)
(40)
Use the given transformation to evaluate the integral. 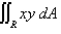 , where R is the region in the first quadrant bounded by the lines
, where R is the region in the first quadrant bounded by the lines 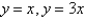 and the hyperbolas
and the hyperbolas 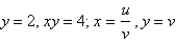 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Use spherical coordinates.Evaluate 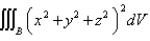 , where
, where 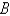 is the ball with center the origin and radius
is the ball with center the origin and radius 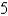 .
.
(Multiple Choice)
4.8/5  (39)
(39)
Evaluate the double integral. 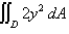 ,
, 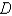 is triangular region with vertices
is triangular region with vertices 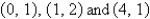 .
.
(Short Answer)
4.7/5  (38)
(38)
Use spherical coordinates to find the volume of the solid that lies within the sphere 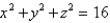 above the xy-plane and below the cone
above the xy-plane and below the cone 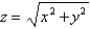 . Round the answer to two decimal places.
. Round the answer to two decimal places.
(Short Answer)
4.9/5  (37)
(37)
Use cylindrical coordinates to evaluate 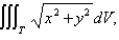 where T is the solid bounded by the cylinder
where T is the solid bounded by the cylinder 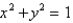 and the planes
and the planes 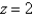 and
and 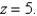
(Multiple Choice)
4.7/5  (32)
(32)
Express the triple integral 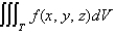 as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes
as an iterated integral in six different ways using different orders of integration where T is the solid bounded by the planes 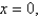
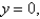
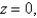 and
and 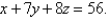
(Short Answer)
4.8/5  (31)
(31)
Use the transformation 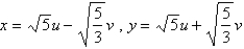 to evaluate the integral
to evaluate the integral 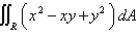 , where R is the region bounded by the ellipse
, where R is the region bounded by the ellipse 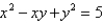 .
.
(Multiple Choice)
4.7/5  (35)
(35)
Use a triple integral to find the volume of the solid bounded by 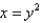 and the planes
and the planes 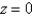 and
and 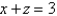 .
.
(Multiple Choice)
4.8/5  (41)
(41)
Determine whether to use polar coordinates or rectangular coordinates to evaluate the integral 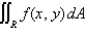 , where f is a continuous function. Then write an expression for the (iterated) integral.
, where f is a continuous function. Then write an expression for the (iterated) integral. 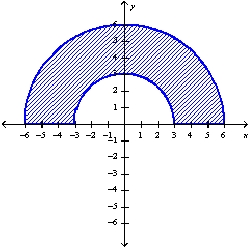
(Short Answer)
4.8/5  (33)
(33)
Find the mass of the solid S bounded by the paraboloid 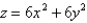 and the plane
and the plane 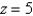 if S has constant density 3.
if S has constant density 3.
(Multiple Choice)
4.7/5  (29)
(29)
Evaluate the integral by making an appropriate change of variables. Round your answer to two decimal places. 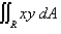 R is the parallelogram bounded by the lines
R is the parallelogram bounded by the lines 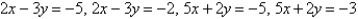 .
.
(Short Answer)
4.9/5  (37)
(37)
Find the mass of the solid E, if E is the cube given by 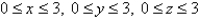 and the density function
and the density function 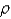 is
is 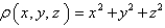 .
.
(Short Answer)
4.8/5  (32)
(32)
Evaluate the double integral. 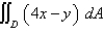
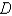 is bounded by the circle with center the origin and radius
is bounded by the circle with center the origin and radius 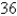 .
.
(Short Answer)
4.9/5  (45)
(45)
Showing 21 - 40 of 59
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)