Exam 16: Oscillations
Exam 1: Getting Started24 Questions
Exam 2: One-Dimensional Motion66 Questions
Exam 3: Vectors47 Questions
Exam 4: Two- and Three-Dimensional Motion79 Questions
Exam 5: Newtons Laws of Motion103 Questions
Exam 6: Applications of Newtons Laws of Motion64 Questions
Exam 7: Gravity47 Questions
Exam 8: Conservation of Energy31 Questions
Exam 9: Energy in Nonisolated Systems41 Questions
Exam 10: Systems of Particles and Conservation of Momentum25 Questions
Exam 11: Collisions43 Questions
Exam 12: Rotation I: Kinematics and Dynamics65 Questions
Exam 13: Rotation II: a Conservation Approach42 Questions
Exam 14: Static Equilibrium, Elasticity, and Fracture34 Questions
Exam 15: Fluids53 Questions
Exam 16: Oscillations41 Questions
Exam 17: Traveling Waves46 Questions
Exam 18: Superposition and Standing Waves56 Questions
Exam 19: Temperature, Thermal Expansion, and Gas Laws45 Questions
Exam 20: Kinetic Theory of Gases19 Questions
Exam 21: Heat and the First Law of Thermodynamics35 Questions
Exam 22: Entropy and the Second Law of Thermodynamics55 Questions
Exam 23: Electric Forces34 Questions
Exam 24: Electric Fields48 Questions
Exam 25: Gausss Law80 Questions
Exam 26: Electric Potential96 Questions
Exam 27: Capacitors and Batteries63 Questions
Exam 28: Current and Resistance32 Questions
Exam 29: Direct Current Dc Circuits84 Questions
Exam 30: Magnetic Fields and Forces75 Questions
Exam 31: Gausss Law for Magnetism and Amperes Law87 Questions
Exam 32: Faradays Law of Induction56 Questions
Exam 33: Inductors and Ac Circuits86 Questions
Exam 34: Maxwells Equations and Electromagnetic Waves41 Questions
Exam 35: Diffraction and Interference48 Questions
Exam 36: Applications of the Wave Model31 Questions
Exam 37: Reflection and Images Formed by Reflection25 Questions
Exam 38: Refraction and Images Formed by Refraction54 Questions
Exam 39: Relativity45 Questions
Select questions type
Two circus clowns (each having a mass of 50 kg) swing on two flying trapezes (negligible mass, length 25 m) shown in the figure. At the peak of the swing, one grabs the other, and the two swing back to one platform. The time for the forward and return motion is 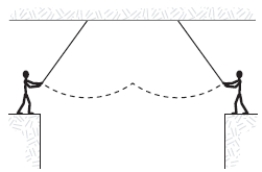
Free
(Multiple Choice)
4.7/5  (39)
(39)
Correct Answer:
A
The mass in the figure slides on a frictionless surface. If m = 2 kg, k1 = 800 N/m and k2 = 500 N/m, the frequency of oscillation (in Hz) is approximately 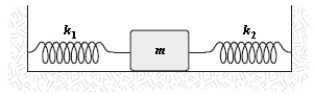
Free
(Multiple Choice)
4.7/5  (30)
(30)
Correct Answer:
C
A torsional pendulum consists of a solid disk (mass = 2.0 kg, radius = 1.0 m) suspended by a wire attached to a rigid support. The body oscillates about the support wire. If the torsion constant is 16 N⋅m/rad. What is the angular frequency (in rad/s)? 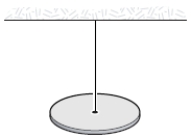
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
B
A uniform rod (mass m = 1.0 kg and length L = 2.0 m) pivoted at one end oscillates in a vertical plane as shown below. The period of oscillation (in s) is approximately 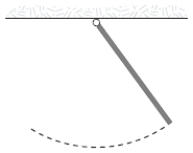
(Multiple Choice)
4.8/5  (30)
(30)
At sea level, at a latitude where 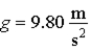 , a pendulum that takes 2.00 s for a complete swing back and forth has a length of 0.993 m. What is the value of g in m/s2 at a location where the length of such a pendulum is 0.970 m?
, a pendulum that takes 2.00 s for a complete swing back and forth has a length of 0.993 m. What is the value of g in m/s2 at a location where the length of such a pendulum is 0.970 m?
(Multiple Choice)
4.8/5  (28)
(28)
Which of the following combinations of variables results in the greatest period for a pendulum?
(Multiple Choice)
4.8/5  (25)
(25)
Three pendulums with strings of the same length and bobs of the same mass are pulled out to angles θ1, θ2, and θ3 respectively, and released. The approximation sin θ = θ holds for all three angles, with θ3 > θ2 > θ1. How do the angular frequencies of the three pendulums compare?
(Multiple Choice)
4.9/5  (47)
(47)
When a damping force is applied to a simple harmonic oscillator which has angular frequency ω0 in the absence of damping, the new angular frequency ω is such that
(Multiple Choice)
4.8/5  (40)
(40)
An automobile (m = 1.00 × 103 kg) is driven into a brick wall in a safety test. The bumper behaves like a spring (k = 5.00 × 106 N/m), and is observed to compress a distance of 3.16 cm as the car is brought to rest. What was the initial speed of the automobile?
(Short Answer)
5.0/5  (41)
(41)
In the figure below, a hoop (radius R = 1.0 m, mass = 2.0 kg) having four spokes of negligible mass is suspended from a pivot a distance d = .25 m above its center of mass. The angular frequency (in rad/s) for small oscillations is approximately 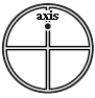
(Multiple Choice)
4.8/5  (39)
(39)
Ellen says that whenever the acceleration is directly proportional to the displacement of an object from its equilibrium position, the motion of the object is simple harmonic motion. Mary says this is true only if the acceleration is opposite in direction to the displacement. Which one, if either, is correct?
(Multiple Choice)
5.0/5  (39)
(39)
In an inertia balance, a body supported against gravity executes simple harmonic oscillations in a horizontal plane under the action of a set of springs. If a 1.00-kg body vibrates at 1.00 Hz, a 2.00-kg body will vibrate at
(Multiple Choice)
4.9/5  (33)
(33)
A hoop, a solid cylinder, and a solid sphere all have the same mass m and the same radius R. Each is mounted to oscillate about an axis a distance 0.5R from the center. The axis is perpendicular to the circular plane of the hoop and the cylinder and to an equatorial plane of the sphere as shown below. Which is the correct ranking in order of increasing angular frequency ω? 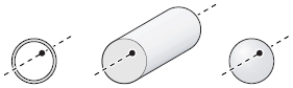
(Multiple Choice)
4.8/5  (34)
(34)
Simple harmonic oscillations can be modeled by the projection of circular motion at constant angular velocity onto a diameter of the circle. When this is done, the analog along the diameter of the acceleration of the particle executing simple harmonic motion is
(Multiple Choice)
4.8/5  (34)
(34)
A body oscillates with simple harmonic motion along the x axis. Its displacement varies with time according to the equation x = 5 sin (πt + π/3). The phase (in rad) of the motion at t = 2 s is
(Multiple Choice)
4.7/5  (35)
(35)
A damped oscillator is released from rest with an initial displacement of 10.00 cm. At the end of the first complete oscillation the displacement reaches 9.05 cm. When 4 more oscillations are completed, what is the displacement reached?
(Multiple Choice)
4.8/5  (40)
(40)
The mat of a trampoline is held by 32 springs, each having a spring constant of 5000 N/m. A person with a mass of 40.0 kg jumps from a platform 1.93 m high onto the trampoline. Determine the stretch of each of the springs.
(Short Answer)
4.9/5  (35)
(35)
A graph of position versus time for an object oscillating at the free end of a horizontal spring is shown below.
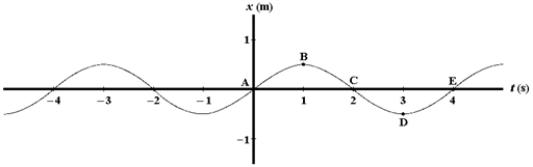
Use this exhibit to answer the following question(s).
-The point at which the object has zero velocity and negative acceleration is
Use this exhibit to answer the following question(s).
-The point at which the object has zero velocity and negative acceleration is
(Multiple Choice)
5.0/5  (37)
(37)
The mass in the figure below slides on a frictionless surface. 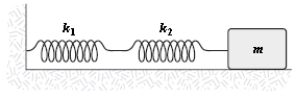 When the mass is pulled out, spring 1 is stretched a distance x1 from its equilibrium position and spring 2 is stretched a distance x2. The spring constants are k1 and k2, respectively. The force pulling back on the mass is
When the mass is pulled out, spring 1 is stretched a distance x1 from its equilibrium position and spring 2 is stretched a distance x2. The spring constants are k1 and k2, respectively. The force pulling back on the mass is
(Multiple Choice)
4.9/5  (38)
(38)
A graph of position versus time for an object oscillating at the free end of a horizontal spring is shown below.

Use this exhibit to answer the following question(s).
-A point or points at which the object has positive velocity and zero acceleration is(are)
Use this exhibit to answer the following question(s).
-A point or points at which the object has positive velocity and zero acceleration is(are)
(Multiple Choice)
4.9/5  (27)
(27)
Showing 1 - 20 of 41
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)