Exam 3: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Determine whether the scatter plot below could best be modeled by a linear model, a quadratic model, an exponential model, a logarithmic model, or a logistic model. 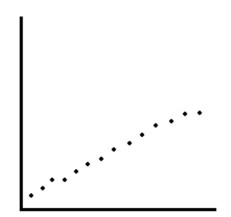
(Multiple Choice)
4.8/5  (38)
(38)
The sales S (in thousands of units) of a cleaning solution after x hundred dollars is spent on advertising are given by When $450 is spent on advertising, 2500 Units are sold. Complete the model by solving for k and use the model to estimate the Number of units that will be sold if advertising expenditures are raised to $650. Round Your answer to the nearest unit.
(Multiple Choice)
4.9/5  (36)
(36)
Use the properties of logarithms to expand the expression as a sum, difference, and/or constant multiple of logarithms. (Assume all variables are positive.)
(Multiple Choice)
5.0/5  (38)
(38)
Condense the expression below to the logarithm of a single quantity.
(Multiple Choice)
4.9/5  (37)
(37)
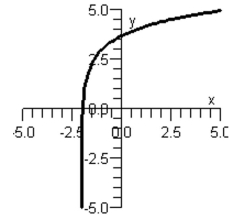
Match the function with its graph.
Graph I:
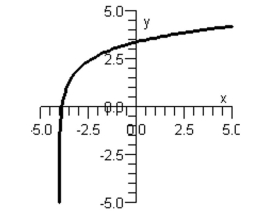 Graph II:
Graph II:
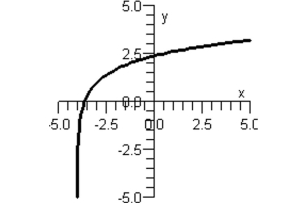 Graph III:
Graph III:
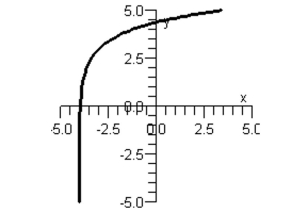 Graph IV:
Graph IV:
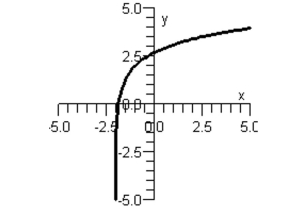 Graph V:
Graph V:
(Multiple Choice)
4.9/5  (26)
(26)
Use the properties of logarithms to expand the expression as a sum, difference, and/or constant multiple of logarithms. (Assume all variables are positive.)
(Multiple Choice)
5.0/5  (38)
(38)
Solve the equation below algebraically. Round your result to three decimal places.
(Multiple Choice)
4.7/5  (37)
(37)
Solve the logarithmic equation below algebraically. Round your result to three decimal places.
(Multiple Choice)
4.7/5  (34)
(34)
Showing 81 - 100 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)