Exam 9: Topics in Analytic Geometry
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Use the Quadratic Formula to solve for y in the following equation.
(Multiple Choice)
4.8/5  (45)
(45)
Use a graphing utility to graph the rotated conic.
Use either grid below for your graph, whichever is more convenient.
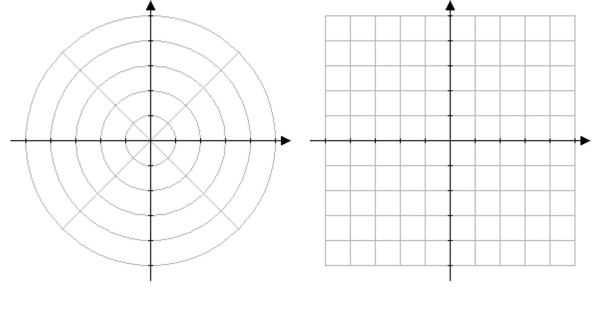
(Essay)
4.8/5  (40)
(40)
A projectile is launched from ground level at an angle of with the horizontal. The initial velocity is feet per second and the path of the projectile is modeled by the parametric equations
Use a graphing utility to graph the paths of a projectile launched from ground level with the values given for and . Use the graph to approximate the maximum height and range of the projectile to the nearest foot.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the following system of quadratic equations algebraically by the method of substitution.
(Multiple Choice)
4.7/5  (36)
(36)
Use the discriminant to classify the graph; then use the quadratic formula to solve for y.
(Multiple Choice)
4.8/5  (36)
(36)
Find a polar equation of the conic with the given characteristics and with one focus at the pole. Conic Eccentricity Directrix Hyperbola e=5 x=2
(Multiple Choice)
4.8/5  (28)
(28)
Rotate the axes to eliminate the -term in the equation. Then write the equation in standard form.
(Multiple Choice)
4.8/5  (36)
(36)
Classify the graph of the equation below as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.8/5  (29)
(29)
Which answer is a polar form of the given rectangular equation?
(Multiple Choice)
4.7/5  (45)
(45)
Find the standard form of the equation of the ellipse centered at the origin having vertices at and and foci at and .
(Multiple Choice)
4.9/5  (31)
(31)
Find the standard form of the parabola with the given characteristics.
directrix:
vertex:
(Multiple Choice)
4.9/5  (53)
(53)
Find the standard form of the equation of the ellipse with the following characteristics.
foci: major axis of length: 22
(Multiple Choice)
5.0/5  (35)
(35)
Which answer is a polar form of the given rectangular equation?
(Multiple Choice)
4.8/5  (39)
(39)
Classify the graph of the equation below as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.8/5  (37)
(37)
Find a polar equation of the conic with the given characteristics and with one focus at the pole. Conic Eccentricity Directrix Parabola e=1 x=-4
(Multiple Choice)
4.8/5  (34)
(34)
Convert the point from polar coordinates to rectangular coordinates. Round answer to three decimal places, if necessary.
(Multiple Choice)
4.9/5  (41)
(41)
Showing 41 - 60 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)