Exam 9: Topics in Analytic Geometry
Exam 1: Functions and Their Graphs118 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions120 Questions
Exam 4: Trigonometric Functions118 Questions
Exam 5: Analytic Trigonometry120 Questions
Exam 6: Additional Topics in Trigonometry120 Questions
Exam 7: Linear Systems and Matrices120 Questions
Exam 8: Sequences, Series, and Probability119 Questions
Exam 9: Topics in Analytic Geometry120 Questions
Exam 10: Analytic Geometry in Three Dimensions120 Questions
Exam 11: Limits and an Introduction to Calculus40 Questions
Exam 12: Review of Graphs, Equations, and Inequalities99 Questions
Select questions type
Find the eccentricity of the following ellipse. Round your answer to two decimals. 0
(Multiple Choice)
4.8/5  (43)
(43)
Classify the graph of the equation below as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.8/5  (32)
(32)
Which set of parametric equations represents the following line or conic?
Use and .
Line: passes through and
(Multiple Choice)
4.8/5  (41)
(41)
Test the graph of the following equation for symmetry with respect to , the polar axis, and the pole.
(Multiple Choice)
4.7/5  (37)
(37)
Find the eccentricity of the following ellipse. Round your answer to two decimals.
(Multiple Choice)
4.9/5  (42)
(42)
Find the standard form of the parabola with the given characteristic and vertex at the origin.
directrix:
(Multiple Choice)
4.7/5  (40)
(40)
Planets travel in elliptical orbits with the sun at one focus. Assume that the focus is at the pole, the major axis lies on the polar axis, and the length of the major axis is (see figure). The polar equation of the orbit of a planet is given below, where is the eccentricity. If miles and , find the perihelion distance (the minimum distance from the sun to the planet). Round your answer to the nearest mile.
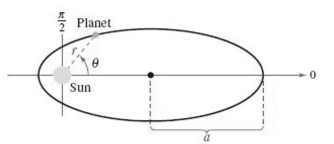
(Multiple Choice)
4.8/5  (43)
(43)
Classify the graph of the equation below as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.9/5  (35)
(35)
Find three additional polar representations of the point , given in polar coordinates, using .
(Multiple Choice)
4.8/5  (40)
(40)
Test the graph of the following equation for symmetry with respect to , the polar axis, and the pole.
(Multiple Choice)
4.8/5  (40)
(40)
Find the standard form of the equation of the ellipse with the given characteristics. foci: endpoints of the major axis:
(Multiple Choice)
4.9/5  (39)
(39)
Which set of parametric equations represents the graph of the following rectangular equation using ?
(Multiple Choice)
4.8/5  (39)
(39)
Find the standard form of the equation of the ellipse below.
(Multiple Choice)
4.9/5  (37)
(37)
Test for symmetry with respect to , the polar axis, and the pole.
(Multiple Choice)
4.8/5  (31)
(31)
Find the standard form of the equation of the ellipse with the following characteristics.
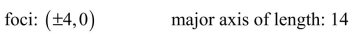
(Multiple Choice)
4.9/5  (32)
(32)
Rotate the axes to eliminate the -term in the following equation and then write the equation in standard form.
(Multiple Choice)
4.8/5  (27)
(27)
Showing 81 - 100 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)