Exam 18: Repeated-Measures Analysis of Variance

If the assumption of constant correlations in a repeated-measures ANOVA is violated, which of the following is true?

The next few questions are based on the following summary table. 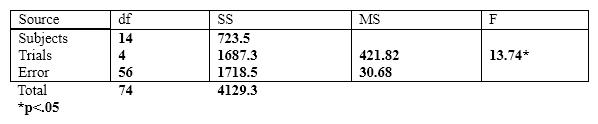The error term in this analysis could also be thought of as

In an example in the text, an independent samples analysis of variance example from a previous chapter was converted to be used in a repeated-measures analysis of variance. Recalculating the F value with a repeated-measures analysis of variance yields an F value that is

The major disadvantage with repeated-measures designs is that they

The next few questions are based on the following summary table. 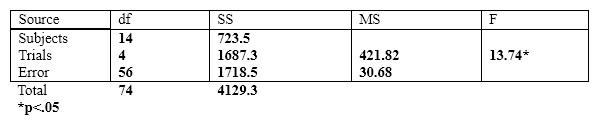The MS _error = 30.68 tells us that

A design in which each subject receives all levels of an independent variable is called a(n)

If we ran a repeated-measures analysis of variance to track changes in patients' distorted thoughts over 6 weeks of therapy, we would most likely want to report the effect size in terms of

On the following computer output, the significance of F varies depending on which test you look at. 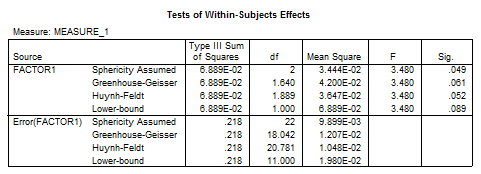a. Why is this the case? b. Which F value should be reported? Explain your answer.

The next few questions are based on the following summary table. 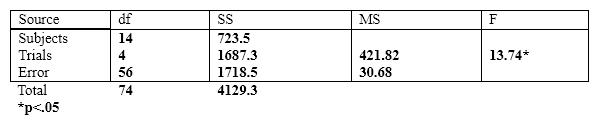If we used a Bonferroni test to run multiple comparisons in the above example, the error term that we would use would be

In a repeated-measures design, SS_error is calculated the same as it is in a between-subjects design.

The next few questions are based on the following summary table. 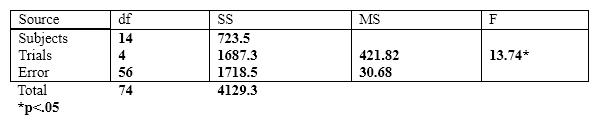We don't have an F test on Subjects. What harm does that do?

If both the Greenhouse and Geisser and the Huynh and Feldt corrections lead to significant results we should

Give two examples in which you might use a repeated-measures design.

The next few questions are based on the following summary table. 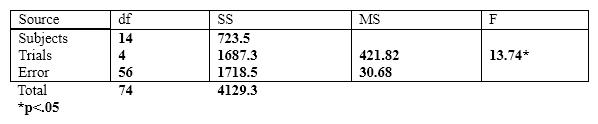If we wanted to run a set of multiple comparisons on the data analyzed in the summary table above, we could use

In a typical learning experiment, a carry-over effect is

In the printout of results for a repeated-measures analysis of variance, an F score for "mean" or "constant" sometimes appears. Why is this statistic often not interesting even if it is significant?

The next few questions are based on the following summary table. 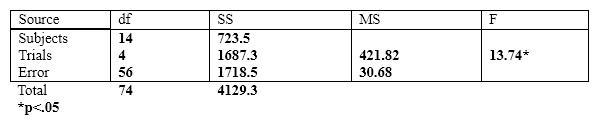How many subjects were involved in this study?

The text used an example in which the author rearranged the data points to look as if they came from a repeated-measures design. In real life we would not move our data points around so that we could analyze them as repeated measures. Why not?

Some summary tables include a term labeled "mean" or "constant," with a corresponding F test. This tests the hypothesis that

A researcher examined reaction time in 12 people across 3 conditions: regular cola, caffeine free cola, and water. The overall F was significant, so she performed multiple comparisons to understand which conditions differed. Interpret the following multiple comparisons at the .05 level. 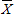_cola = 2.43s, 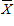_{caffeine free} = 2.52s, 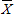_water = 2.53s.  t_{cola/caffeine free} = 2.80; t_cola/water = 2.17;  t _{water/caffeine free} = 0.38