Exam 1: Systems of Linear Equations
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
Determine if the system is in echelon form, and if so, identify the leading variables and the free variables. If it is not in echelon form, explain why.
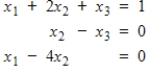
(Short Answer)
4.8/5  (31)
(31)
Find the equilibrium temperatures for the heavy wires with endpoints held at the given temperatures.
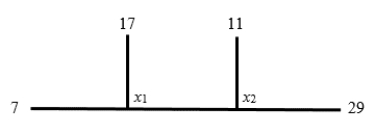
(Essay)
4.9/5  (38)
(38)
Compute the first three Gauss-Seidel iterations for the system in question 5, using
 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
(Essay)
4.9/5  (31)
(31)
Find all possible equilibrium and endpoint temperatures for the heavy wires with endpoints held at the indicated temperatures.
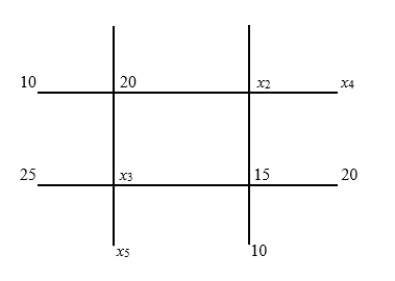
(Essay)
4.8/5  (31)
(31)
Determine whether the matrix is in reduced echelon form, echelon form only, or not in echelon form.
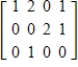
(Short Answer)
4.8/5  (39)
(39)
Convert the given system to an augmented matrix, and find all solutions by reducing to echelon form and using back substitution , if needed.
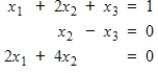
(Essay)
4.8/5  (30)
(30)
Identify the row operation which transforms the matrix on the left to the matrix on the right.
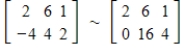
(Essay)
4.8/5  (37)
(37)
Determine whether the matrix is in reduced echelon form, echelon form only, or not in echelon form.

(Short Answer)
4.9/5  (37)
(37)
Compute the first three Jacobi iterations, using
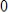 as the initial value for each variable. Then find the exact solution and compare.
as the initial value for each variable. Then find the exact solution and compare.
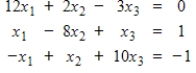
(Essay)
4.8/5  (38)
(38)
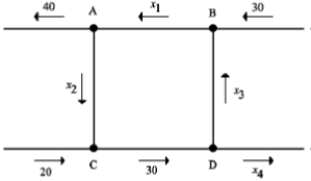
The volume of traffic for a collection of intersections is shown. Find all possible values for
 ,
,
 ,
,
 , and
, and
 .
.
(Essay)
4.8/5  (28)
(28)
Solve the given system using Gaussian elimination with three significant digits of accuracy. Then solve the system again, incorporating partial pivoting.
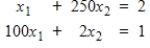
(Essay)
4.9/5  (36)
(36)
Use partial pivoting with Gaussian elimination to find the solutions to the system.
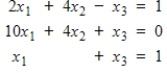
(Essay)
4.8/5  (29)
(29)
Determine which of the points (1, 0, -1, 0), (0, 1, 2, 3), and (2, 1, -1, -1) satisfy the linear system
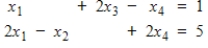
(Short Answer)
4.8/5  (32)
(32)
Determine the value(s) of
 so that the following system is consistent.
so that the following system is consistent.
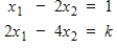
(Essay)
4.7/5  (32)
(32)
The volume of traffic for a collection of intersections is shown. Find the minimum volume of traffic from C to D. 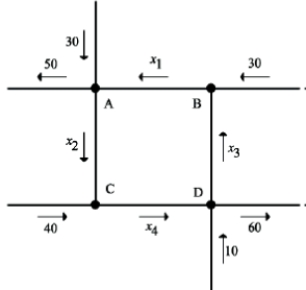
(Essay)
5.0/5  (30)
(30)
Showing 41 - 57 of 57
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)