Exam 6: Discrete Probability Distributions
Exam 1: Data Collection34 Questions
Exam 2: Organizing and Summarizing Data30 Questions
Exam 3: Numerically Summarizing Data66 Questions
Exam 4: Describing the Relation Between Two Variables92 Questions
Exam 5: Probability91 Questions
Exam 6: Discrete Probability Distributions32 Questions
Exam 7: The Normal Probability Distributions36 Questions
Exam 8: Sampling Distributions12 Questions
Exam 9: Estimating the Value of a Parameter Using Confidence Intervals24 Questions
Exam 10: Hypothesis Tests Regarding a Parameter36 Questions
Exam 11: Inference on Two Samples65 Questions
Exam 12: Inference on Categorical Data16 Questions
Exam 13: Comparing Three or More Means15 Questions
Exam 14: Inference of the Least-Squares Regression Model28 Questions
Select questions type
An Apple Pie Company knows that the number of pies sold each day varies from day to day. The owner believes that on 50% of the days she sells 100 pies. On another 25% of the days she sells 150 pies, and she sells 200 pies on the remaining 25% of the days. To make sure she has enough product, the owner bakes 200 pies each day at a cost of $2.50 each. Assume any pies that go unsold are thrown out at the end of the day. If she sells the pies for $5 each, find the probability distribution for her daily profit.
Free
(Multiple Choice)
4.9/5  (43)
(43)
Correct Answer:
D
Given the table of probabilities for the random variable x, does this form a probability distribution? 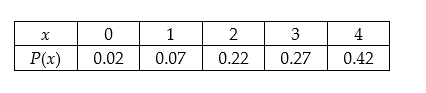
Free
(True/False)
5.0/5  (45)
(45)
Correct Answer:
True
The random variable x represents the number of computers that families have along with the corresponding probabilities. Find the mean and standard deviation for the random variable x. 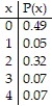
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Suppose x is a random variable for which a Poisson probability distribution with 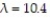 provides a good characterization. Find ? for x.
provides a good characterization. Find ? for x.
(Multiple Choice)
4.7/5  (31)
(31)
A seed company has a test plot in which it is testing the germination of a hybrid seed. They plant 50 rows of 40 seeds per row. After a two-week period, the researchers count how many seed per row have sprouted. They noted that least number of seeds to germinate was 33 and some rows had all 40 germinate. The germination data is given below in the table. The random variable x represents the number of seed in a row that germinated and P(x) represents the probability of selecting a row with that number of seed germinating. Determine the standard deviation of the number of seeds per row that germinated. 
(Multiple Choice)
4.9/5  (53)
(53)
The probability that an individual has 20-20 vision is 0.12. In a class of 43 students, what is the probability of finding five people with 20-20 vision?
(Multiple Choice)
4.9/5  (41)
(41)
A legendary football coach was known for his winning seasons. He consistently won nine or more games per season. Suppose x equals the number of games won up to the halfway mark (six games) in a  season. If this coach and his team had a probability
season. If this coach and his team had a probability 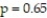 of winning any one game (and the winning or losing of one game was independent of another), then the probability distribution of the number x of winning games in a series of six games is:
of winning any one game (and the winning or losing of one game was independent of another), then the probability distribution of the number x of winning games in a series of six games is:  Find the expected number of winning games in the first half of the season for this coach's football teams.
Find the expected number of winning games in the first half of the season for this coach's football teams.
(Essay)
4.8/5  (34)
(34)
The owner of a farmer's market was interested in determining how many oranges a person buys when they buy oranges. He asked the cashiers over a weekend to count how many oranges a person bought when they bought oranges and record this number for analysis at a later time. The data is given below in the table. The random variable x represents the number of oranges purchased and P(x) represents the probability that a customer will buy x oranges. Determine the variance of the number of oranges purchased by a customer. 
(Multiple Choice)
4.8/5  (40)
(40)
The random variable x represents the number of tests that a patient entering a clinic will have along with the corresponding probabilities. Find the mean and standard deviation for the random variable x. 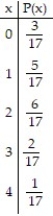
(Multiple Choice)
4.9/5  (44)
(44)
A lab orders a shipment of 100 rats a week, 52 weeks a year, from a rat supplier for experiments that the lab conducts. Prices for each weekly shipment of rats follow the distribution below:
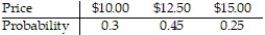 How much should the lab budget for next year's rat orders assuming this distribution does not change. (Hint: find the expected price.)
How much should the lab budget for next year's rat orders assuming this distribution does not change. (Hint: find the expected price.)
(Multiple Choice)
4.9/5  (39)
(39)
A psychic network received telephone calls last year from over 1.5 million people. A recent article attempts to shed some light onto the credibility of the psychic network. One of the psychic network's psychics agreed to take part in the following experiment. Five different cards are shuffled, and one is chosen at random. The psychic will then try to identify which card was drawn without seeing it. Assume that the experiment was repeated 50 times and that the results of any two experiments are independent of one another. If we assume that the psychic is a fake (i.e., they are merely guessing at the cards and have no psychic powers), how many of the 50 cards do we expect the psychic to guess correctly?
(Multiple Choice)
4.8/5  (48)
(48)
The produce manager at a farmer's market was interested in determining how many oranges a person buys when they buy oranges. He asked the cashiers over a weekend to count how many oranges a person bought when they bought oranges and record this number for analysis at a later time. The data is given below in the table. The random variable x represents the number of oranges purchased and P(x) represents the probability that a customer will buy x apples. Determine the mean number of oranges purchased by a customer. 
(Multiple Choice)
4.8/5  (38)
(38)
Given the table of probabilities for the random variable x, does this form a probability distribution? 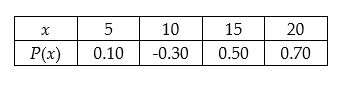
(True/False)
4.7/5  (36)
(36)
If p is the probability of success of a binomial experiment, then the probability of failure is
(Multiple Choice)
4.8/5  (33)
(33)
According to the Federal Communications Commission, 70% of all U.S. households have vcrs. In a random sample of 15 households, what is the probability that fewer than 13 have vcrs?
(Multiple Choice)
4.9/5  (41)
(41)
Consider the discrete probability distribution to the right when answering the following question. Find the probability that x exceeds 4. 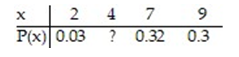
(Multiple Choice)
4.9/5  (31)
(31)
A recent article in the paper claims that government ethics are at an all-time low. Reporting on a recent sample, the paper claims that 32% of all constituents believe their representative possesses low ethical standards. Assume that responses were randomly and independently collected. A representative of a district with 1,000 people does not believe the paper's claim applies to her. If the claim is true, how many of the representative's constituents believe the representative possesses low ethical standards?
(Multiple Choice)
4.8/5  (44)
(44)
The peak shopping time at home improvement store is between 8:00am-11:00 am on Saturday mornings. Management at the home improvement store randomly selected 175 customers last Saturday morning and decided to observe their shopping habits. They recorded the number of items that each of the customers purchased as well as the total time the customers spent in the store. Identify the types of variables recorded by the home improvement store.
(Multiple Choice)
4.9/5  (42)
(42)
Consider the discrete probability distribution to the right when answering the following question. Find the probability that x equals 4. 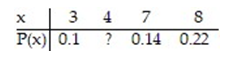
(Multiple Choice)
5.0/5  (30)
(30)
A lab orders a shipment of 100 rats a week, 52 weeks a year, from a rat supplier for experiments that the lab conducts. Prices for each weekly shipment of rats follow the distribution below:
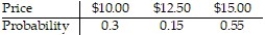 Suppose the mean cost of the rats turned out to be $13.13 per week. Interpret this value.
Suppose the mean cost of the rats turned out to be $13.13 per week. Interpret this value.
(Multiple Choice)
4.8/5  (30)
(30)
Showing 1 - 20 of 32
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)