Exam 6: Discrete Probability Distributions
Exam 1: Data Collection34 Questions
Exam 2: Organizing and Summarizing Data30 Questions
Exam 3: Numerically Summarizing Data66 Questions
Exam 4: Describing the Relation Between Two Variables92 Questions
Exam 5: Probability91 Questions
Exam 6: Discrete Probability Distributions32 Questions
Exam 7: The Normal Probability Distributions36 Questions
Exam 8: Sampling Distributions12 Questions
Exam 9: Estimating the Value of a Parameter Using Confidence Intervals24 Questions
Exam 10: Hypothesis Tests Regarding a Parameter36 Questions
Exam 11: Inference on Two Samples65 Questions
Exam 12: Inference on Categorical Data16 Questions
Exam 13: Comparing Three or More Means15 Questions
Exam 14: Inference of the Least-Squares Regression Model28 Questions
Select questions type
A dice game involves throwing three dice and betting on one of the six numbers that are on the dice. The game costs $11 to play, and you win if the number you bet appears on any of the dice. The distribution for the outcomes of the game (including the profit) is shown below:  Find your expected profit from playing this game.
Find your expected profit from playing this game.
(Multiple Choice)
4.9/5  (40)
(40)
A psychic network received telephone calls last year from over 1.5 million people. A recent article attempts to shed some light onto the credibility of the psychic network. One of the psychic network's psychics agreed to take part in the following experiment. Five different cards are shuffled, and one is chosen at random. The psychic will then try to identify which card was drawn without seeing it. Assume that the experiment was repeated 45 times and that the results of any two experiments are independent of one another. If we assume that the psychic is a fake (i.e., they are merely guessing at the cards and have no psychic powers), find the probability that they guess at least three correctly.
(Multiple Choice)
4.8/5  (32)
(32)
Calculate the mean for the discrete probability distribution shown here. 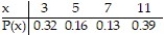
(Multiple Choice)
4.9/5  (38)
(38)
A seed company has a test plot in which it is testing the germination of a hybrid seed. They plant 50 rows of 40 seeds per row. After a two-week period, the researchers count how many seed per row have sprouted. They noted that least number of seeds to germinate was 33 and some rows had all 40 germinate. The germination data is given below in the table. The random variable x represents the number of seed in a row that germinated and P(x) represents the probability of selecting a row with that number of seed germinating. Determine the mean number of seeds per row that germinated.

(Multiple Choice)
5.0/5  (37)
(37)
In a sandwich shop, the following probability distribution was obtained. The random variable x represents the number of condiments used for a hamburger. Find the mean and standard deviation for the random variable x. 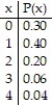
(Multiple Choice)
4.9/5  (34)
(34)
On one busy holiday weekend, a national airline has many requests for standby flights at half of the usual one-way air fare. However, past experience has shown that these passengers have only about a 1 in 5 chance of getting on the standby flight. When they fail to get on a flight as a standby, their only other choice is to fly first class on the next flight out. Suppose that the usual one-way air fare to a certain city is $124 and the cost of flying first class is $385. Should a passenger who wishes to fly to this city opt to fly as a standby? [Hint: Find the expected cost of the trip for a person flying standby.]
(Essay)
5.0/5  (34)
(34)
An automobile insurance company estimates the following loss probabilities for the next year on a $25,000 sports car: 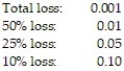 Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage), how much annual premium should the company charge in order to average $500 profit per policy sold?
Assuming the company will sell only a $500 deductible policy for this model (i.e., the owner covers the first $500 damage), how much annual premium should the company charge in order to average $500 profit per policy sold?
(Essay)
4.7/5  (38)
(38)
A recent article in the paper claims that government ethics are at an all-time low. Reporting on a recent sample, the paper claims that 31% of all constituents believe their representative possesses low ethical standards. Suppose 20 of a representative's constituents are randomly and independently sampled. Assuming the paper's claim is correct, find the probability that more than eight but fewer than 12 of the 20 constituents sampled believe their representative possesses low ethical standards.
(Multiple Choice)
4.8/5  (39)
(39)
Suppose the number of babies born during an 8-hour shift at a hospital's maternity wing follows a Poisson distribution with a mean of 3 an hour. Some people believe that the presence of a full moon increases the number of births that take place. Suppose during the presence of a full moon, County Hospital experienced eight consecutive hours with more than four births. Based on this fact, comment on the belief that the full moon increases the number of births.
(Multiple Choice)
4.8/5  (37)
(37)
A manager asked her employees how many times they had given blood in the last year. The results of the survey are given below. The random variable x represents the number of times a person gave blood and P(x) represents the probability of selecting an employee who had given blood that percent of the time. What is the mean number of times a person gave blood based on this survey? 
(Multiple Choice)
4.9/5  (44)
(44)
A manager at a local company asked his employees how many times they had given blood in the last year. The results of the survey are given below. The random variable x represents the number of times a person gave blood and P(x) represents the probability of selecting an employee who had given blood that percent of the time. What is the standard deviation for the number of times a person gave blood based on this survey? 
(Multiple Choice)
4.9/5  (39)
(39)
Showing 21 - 32 of 32
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)