Exam 5: Linear Programming: Sensitivity Analysis, Duality, and Specialized Models
Exam 1: Introduction to Management Science, Modeling, and Excel Spreadsheets33 Questions
Exam 2: Forecasting75 Questions
Exam 3: Linear Programming: Basic Concepts and Graphical Solutions59 Questions
Exam 4: Linear Programming: Applications and Solutions61 Questions
Exam 5: Linear Programming: Sensitivity Analysis, Duality, and Specialized Models55 Questions
Exam 6: Transportation, Assignment, and Transshipment Problems53 Questions
Exam 7: Integer Programming58 Questions
Exam 8: Network Optimization Models61 Questions
Exam 9: Nonlinear Optimization Models60 Questions
Exam 10: Multi-Criteria Models60 Questions
Exam 11: Decision Theory59 Questions
Exam 12: Markov Analysis52 Questions
Exam 13: Waiting Line Models50 Questions
Exam 14: Simulation Cdrom Modules47 Questions
Select questions type
Wilkinson Auto Dealership sells standard automobiles and station wagons. The profit contribution for automobiles is per unit and per unit for station wagons. The company is planning the placement of orders with the manufacturer for next quarter. Orders for automobiles and station wagons can not exceed 320 and 160, respectively. Dealer preparation takes 2 hrs/auto and 5.0 hrs/wagon. They have 1100 hrs of preparation time next quarter. Autos take 1 unit of space, whereas wagons take 1.2 units of space. 480 units of space are available. In order to maintain some balance, the number of cars ordered should not be more than the number of wagons ordered. Assume that they can sell all the autos and wagons they order for the quarter. The formulation of the problem is given below. Using excel-solver, completea sensitivity analysis of the objective function coefficients and report on the range of values of the coefficients that will leave the current solution optimal
find the range of feasibility for changes in the RHS of each constraint
Decision variables: Let be the number of automobiles and be the number of station wagons ordered next quarter.
Objective function: Max:
Constraints:
Variables are non-negative
Optimal solution using Solver:
The objective function value corresponding to the optimal solution is:
Free
(Essay)
4.9/5  (36)
(36)
Correct Answer:
(A) Output from sensitivity analysis is given below:
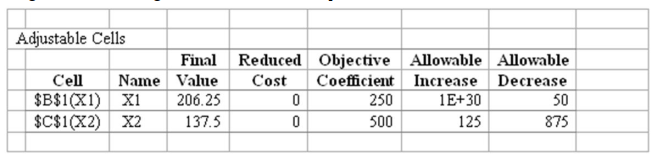 Using this data, the range on the coefficient of is:
Using this data, the range on the coefficient of is:
Similarly, range on the coefficient of is:
(B) Output for the ranges of feasibility of RHS from solver is given below:
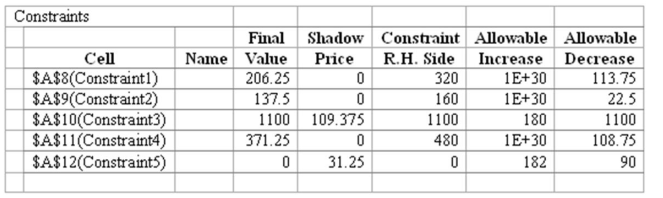 RHS
RHS
RHS
RHS3
RHS
RHS5
In a two-variable graphical linear program, if the RHS of one of the constraints is changed (keeping all other things fixed), then the problem cannot become infeasible.
Free
(True/False)
4.7/5  (30)
(30)
Correct Answer:
False
The value of may be included as part of the range produced by sensitivity analysis in some problems.
Free
(True/False)
5.0/5  (40)
(40)
Correct Answer:
True
Given the following linear programming problem with two non-negative variables and , find the range of feasibility for the RHS of constraint 1 (hint: both constraints are not binding)
Max:
Constraints:
Variables are non-negative
(Multiple Choice)
4.7/5  (39)
(39)
Given the following linear programming problem with two non-negative variables and constraints (all type), and a maximize objective function , where , respective to the dual variables associated with constraints 1,2 and 3 ),
Max:
Constraints:
Variables are non-negative
One of the constraints of the dual problem is
(Multiple Choice)
4.8/5  (34)
(34)
Given the following linear programming problem with two non-negative variables and , find the range of values for the objective function coefficient of that will leave the current solution optimal (that is range of optimality or range of insignificance as the case may be) (hint: both constraints are not binding)
Max:
Constraints:
Variables are non-negative
(Multiple Choice)
4.7/5  (40)
(40)
Given the following linear programming problem with two non-negative variables and , find the range of values for the objective function coefficient of that will leave the current solution optimal (that is range of optimality or range of insignificance as the case may be) (hint: both constraints are binding)
Max:
Constraints:
Variables are non-negative
(Multiple Choice)
4.7/5  (40)
(40)
In order to consider changes to the objective function coefficients and the RHS simultaneously, one can apply the rule - total \% changes must be less than 100 - where negative change is also added without the negative sign.
(True/False)
4.9/5  (33)
(33)
Given the following linear programming problem with two non-negative variables and , 3 constraints (all type), and a maximize objective function , where , respective to the dual variables associated with constraints 1,2 and 3 ),
Max:
Constraints:
Variables are non-negative the objective function of the dual problem is
(Multiple Choice)
4.7/5  (34)
(34)
Sensitivity analysis could be used to estimate the range of values of the right hand side, taken one at a time, that would keep the same variables as the current solution in the optimal solution (same variables basic) - though the magnitude of the variables may change.
(True/False)
4.8/5  (36)
(36)
Find the dual of the following problem:
PRIMAL:
Max:
Subject to:
2+5+3\geq3.02+4+1\leq503+4+2=20 \geq0 \geq0 \geq0
(Essay)
4.9/5  (32)
(32)
The lower bound of the feasibility range of a nonbinding constraint is determined by decreasing the RHS of the constraint by the amount of surplus.
(True/False)
4.8/5  (29)
(29)
In a two-variable linear programming problem, if the RHS corresponding to a binding constraint were to be increased, the value of the variables corresponding to the optimal solution would also change.
(True/False)
4.9/5  (33)
(33)
Given the following linear programming problem with two non-negative variables and , find the range of feasibility for the RHS of constraint 2 (hint: both constraints are not binding)
Max:
Constraints:
Variables are non-negative
(Multiple Choice)
4.9/5  (35)
(35)
Since the solution to the primal problem also contains the solution to the dual problem, there is no need to study dual problems.
(True/False)
4.9/5  (35)
(35)
If a problem has a constraint with a positive RHS, and if that resource is not fully utilized in the optimal solution, then the upper limit on the range using sensitivity analysis for that RHS will be .
(True/False)
5.0/5  (43)
(43)
If the primal problem has maximize objective function, non-negative variables, and 4 constraints, each of which is type, then the dual problem will have 4 variables and all of them will be non-negative.
(True/False)
4.7/5  (34)
(34)
Any linear programming problem can be rewritten as an equivalent linear programming problem with maximize objective function, all constraints and non-negative variables.
(True/False)
4.7/5  (39)
(39)
Sensitivity analysis could be used to estimate the range of values of the coefficient of the constraints, taken one at a time, that would keep the same variables as the current solution, in the optimal solution (same variables basic), though the magnitude of the variables may change.
(True/False)
4.9/5  (47)
(47)
The value of will always be included in any range produced by sensitivity analysis.
(True/False)
4.7/5  (32)
(32)
Showing 1 - 20 of 55
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)