Exam 7: Integer Programming
Exam 1: Introduction to Management Science, Modeling, and Excel Spreadsheets33 Questions
Exam 2: Forecasting75 Questions
Exam 3: Linear Programming: Basic Concepts and Graphical Solutions59 Questions
Exam 4: Linear Programming: Applications and Solutions61 Questions
Exam 5: Linear Programming: Sensitivity Analysis, Duality, and Specialized Models55 Questions
Exam 6: Transportation, Assignment, and Transshipment Problems53 Questions
Exam 7: Integer Programming58 Questions
Exam 8: Network Optimization Models61 Questions
Exam 9: Nonlinear Optimization Models60 Questions
Exam 10: Multi-Criteria Models60 Questions
Exam 11: Decision Theory59 Questions
Exam 12: Markov Analysis52 Questions
Exam 13: Waiting Line Models50 Questions
Exam 14: Simulation Cdrom Modules47 Questions
Select questions type
A common feature of set covering, knapsack, and location problems is that all of them use 0-1 variables.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
True
A cargo plane has two compartments for storing cargo, front and back. These compartments have capacity limits on both weight and space, as summarized below.
 They have three available cargos for an upcoming flight. The details are given below:
They have three available cargos for an upcoming flight. The details are given below:
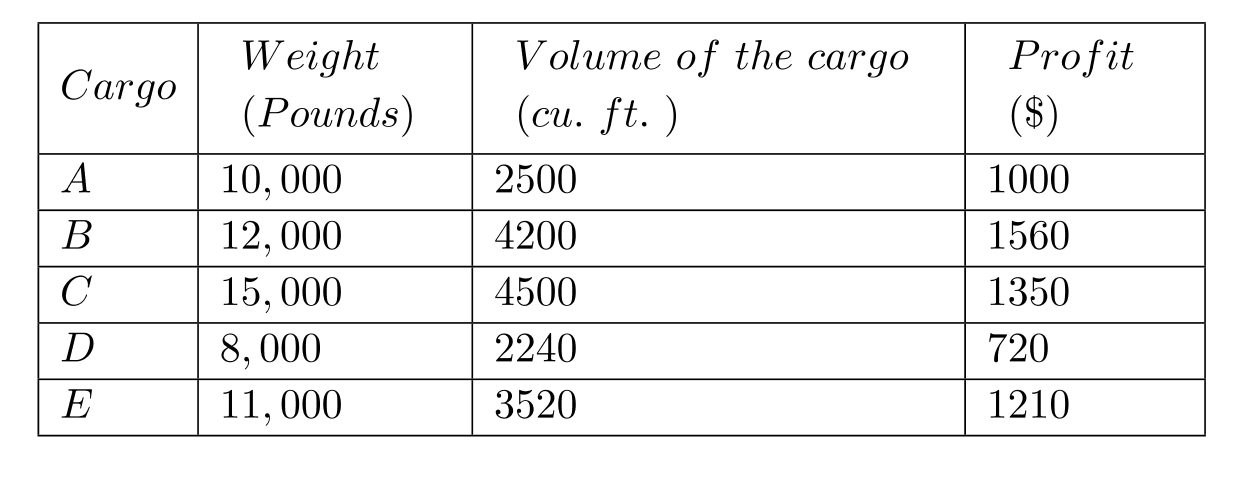 For maintaining balance, the total weight of the cargo loaded in the back must be more than the total cargo loaded in the front. Each cargo must be accepted in full and loaded entirely in front or back. The objective is to determine which must be accepted and where it should go in the plane, so as to maximize total profit. Formulate this as an integer linear program.
For maintaining balance, the total weight of the cargo loaded in the back must be more than the total cargo loaded in the front. Each cargo must be accepted in full and loaded entirely in front or back. The objective is to determine which must be accepted and where it should go in the plane, so as to maximize total profit. Formulate this as an integer linear program.
Free
(Essay)
4.9/5  (35)
(35)
Correct Answer:
Decision variables (a series of 0-1 variables that would take a value of 1 if it is chosen and 0 otherwise):
Let be 1 if cargo i loaded in compartment and 0 otherwise
Objective function:
for and where stands for front and for back
Max:
Variables are
Solver solution:
All other variables are 0 . The objective function value will be equal to
The objective function value corresponding to the optimal solution is
A retail outlet wants to replace a broken ice cream vending machine with one of two models. Purchase of model 1 machine is captured by variable taking a value of 1 and 0 if not purchased. is similarly defined. They would also want to allow for the possibility of getting rid of the old machine with no replacement. One of the constraints for this problem would be
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
B
If a problem contains data on profit as well as cost, it cannot be formulated as an integer programming problem. We have to pick one or the other and then do the formulation.
(True/False)
4.7/5  (37)
(37)
A Mississippi farmer is considering adding a special breed of bull to his farm. Let imply that the bull will be purchased and 0 otherwise. If it is purchased, then the pounds of organic soy purchased per day (denoted by ) and the pounds of organic corn purchased per day (denoted by ) should be at most 50. If the bull is not purchased, then the pounds of organic soy purchased the pounds of organic corn purchased should be at most 30. The constraint/s that implements this would be (M stands for a very big positive number and assume non-negative variables)
(Multiple Choice)
4.9/5  (32)
(32)
A retail outlet wants to replace a broken ice cream vending machine with one of two models. The purchase of model 1 is captured by variable X1, taking a value of 1 and 0 if not purchased. X2 is similarly defined. They would not be opposed to buying both machines, though buying one of them is a must. One of the constraints for this problem would be
(Multiple Choice)
4.9/5  (43)
(43)
In general, we consider more feasible solutions in solving integer linear programming problems. as compared to solving linear programming problems by simplex method.
1.
(True/False)
5.0/5  (32)
(32)
In modeling a traveling salesman problem, let be a 0-1 decision variable, which takes a value of 0 if in the kth leg the tour corresponding to the solution does not go from node to node . is set to be equal to 1 if the tour goes from node to node in the kth leg. In a problem with just 4 nodes and without loss of generality, assume that the tour starts and ends in node 1. Mark the correct constraint to make sure that the tour ends in node 1
(Multiple Choice)
4.9/5  (40)
(40)
In a plant location problem with 5 potential locations, each with an associated 0-1 decision variable, , ,and , which take a value of 1 if a plant is located in that location and 0 otherwise, the constraint to make sure that at least 3 plants are put up will be
(Multiple Choice)
4.7/5  (19)
(19)
A feasible solution to a two-variable pure integer programming problem can always be found by first solving the corresponding linear programming problem (i.e. problem obtained by ignoring the integrality constraints) and by rounding to the nearest integer all fractional values in the optimal solution to the linear programming problem.
(True/False)
4.7/5  (29)
(29)
In modeling a traveling salesman problem, let be a 0-1 decision variable, which takes a value of 0 if in the kth leg the tour corresponding to the solution does not go from node to node . is set to be equal to 1 if the tour goes from node to node in the kth leg. In a problem with just 4 nodes and without loss of generality, assume that the tour starts and ends in node 1 . If, in a particular solution, , it means that the tour corresponding to the solution
(Multiple Choice)
4.8/5  (30)
(30)
For a pure 0-1 integer programming problem with 3 variables, the maximum number of potential solutions is
(Multiple Choice)
4.8/5  (35)
(35)
A feasible solution to a two-variable pure integer programming problem can always be found by first solving the corresponding linear programming problem (i.e. problem obtained by ignoring the integrality constraints) and by rounding down the fractional values in the optimal solution to the linear programming problem.
(True/False)
4.8/5  (32)
(32)
A jumbo jet factory can produce two types of planes\_-UnitMach and BigMach. UnitMach takes 6 man weeks of labor and 7 units of critical machine time. BigMach takes 8 man weeks of labor and 12 units of critical machine time. The total man weeks of labor available during the planning horizon are 50; total units of machine time available during the planning horizon are 70 . Contribution of UnitMach is and BigMach is . Assuming that integer quantities of products should be produced, find the total contribution maximizing solution.
(Essay)
4.8/5  (38)
(38)
Clean Energy Inc. has a planning horizon of 3 years and has 5 potential projects. Each year, the outlay required by each project is known. The amount available for investment in any of these projects each year is also assumed to be known. Each project has an associated expected contribution to total sales whose net present value is also assumed to be known. Determine the project/s that should be undertaken so as to maximize the total net present value of sales subject to budget constraints of each year.
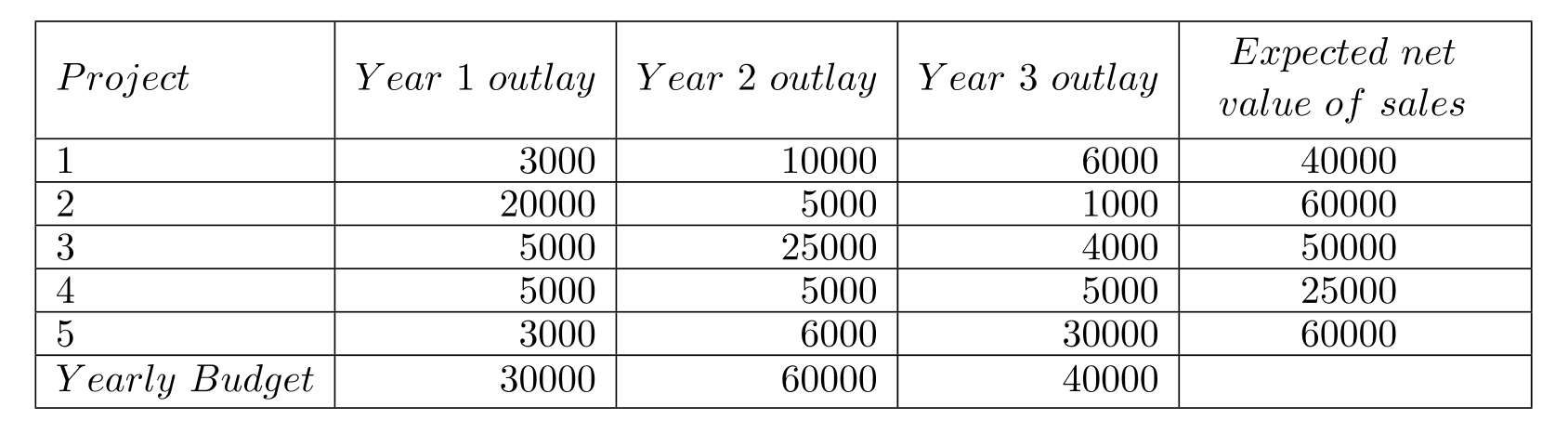
(Essay)
4.9/5  (32)
(32)
A fixed charge problem typically uses , which stands for a very large positive number in its formulation.
(True/False)
5.0/5  (38)
(38)
Sensitivity analysis on the RHS of integer programming problems is relatively easy.
(True/False)
4.9/5  (35)
(35)
A shopping complex is considering building a self-service vending machine island. The mall can buy a vending machine for dispensing various types of ready-to-pop corn. Purchase of this machine is captured by variable , taking a value of 1 and 0 if not purchased. There is also a machine available for popping any type of corn vended by the vending machine. Purchase of this machine is captured by variable X2, taking a value of 1 and 0 if not purchased. Assume that buying just one of these machines does not do much good. That is, either the mall should buy both or buy neither. The constraint that implements this will be
(Multiple Choice)
4.8/5  (42)
(42)
An Avon lady carrying her tote containing makeup materials can maximize her profit from one trip to the rural Mississippi hinterland if she models the process of loading her bag (with the "right" materials having maximum profitability per unit volume) by using a
(Multiple Choice)
4.7/5  (33)
(33)
In modeling a shopping mall construction problem, there are four potential locations giving rise to four 0-1 decision variables, denoted as , which take a value of 1 if a mall is constructed and 0 otherwise. Identify the correct set of constraint/s to satisfy the following condition/s: at least one mall may be constructed among locations 1 and 3
(Multiple Choice)
4.8/5  (34)
(34)
Showing 1 - 20 of 58
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)