Exam 12: Limits, Derivatives, and Definite Integrals
Exam 1: Linear Functions, Equations, and Inequalities44 Questions
Exam 2: Analysis of Graphs of Functions84 Questions
Exam 3: Polynomial Functions40 Questions
Exam 4: Rational, Power, and Root Functions48 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions84 Questions
Exam 6: Systems and Matrices68 Questions
Exam 7: Analytic Geometry and Nonlinear Systems48 Questions
Exam 8: The Unit Circle and Functions of Trigonometry88 Questions
Exam 9: Trigonometric Identities and Equations100 Questions
Exam 10: Applications of Trigonometry and Vectors40 Questions
Exam 11: Further Topics in Algebra48 Questions
Exam 12: Limits, Derivatives, and Definite Integrals100 Questions
Exam 13: Reference: Basic Algebraic Concepts40 Questions
Select questions type
Find the equation of the tangent line to the graph of at the point .
(Short Answer)
4.7/5  (36)
(36)
find the value of the given limit if it exists. If the function approaches or , say so.
-
(Short Answer)
4.9/5  (41)
(41)
find the value of the given limit if it exists. If the function approaches or , say so.
-
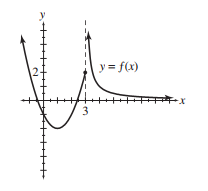
(Short Answer)
4.8/5  (33)
(33)
During a two-week period the number of people in a town who have a virus follows the model , where is the number of people who have the virus after days. Use a calculator to graph for , and determine . What does tell about the situation?
(Essay)
4.8/5  (29)
(29)
find the value of the given limit if it exists. If the function approaches or , say so.
-
(Short Answer)
4.8/5  (33)
(33)
find the value of the given limit if it exists. If the function approaches or , say so.
- where
(Short Answer)
4.9/5  (43)
(43)
Four grams of a radioactive substance is placed in a vault. The function defined by shown in the graph gives the amount remaining after years. At what (in grams per year) is the substance disintegrating after 12 years?
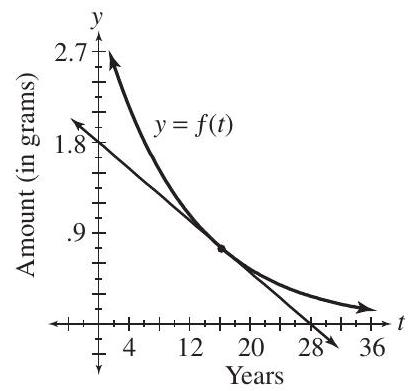
(Short Answer)
4.9/5  (34)
(34)
find the value of the given limit if it exists. If the function approaches or , say so.
-
(Short Answer)
4.7/5  (32)
(32)
Three grams of a radioactive substance is placed in a vault. The function defined by shown in the graph gives the amount remaining after years. At what rate (in grams per year) is the substance disintegrating after 16 years?
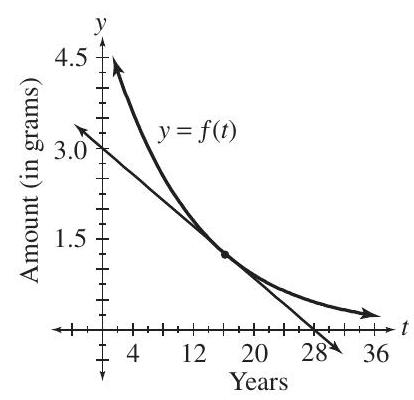
(Short Answer)
4.8/5  (36)
(36)
find the value of the given limit if it exists. If the function approaches or , say so.
-
(Short Answer)
4.8/5  (34)
(34)
find the value of the given limit if it exists. If the function approaches or , say so.
-
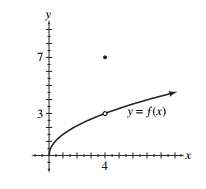
(Short Answer)
4.9/5  (40)
(40)
find the value of the given limit if it exists. If the function approaches or , say so.
-
(Short Answer)
4.7/5  (37)
(37)
Approximate the area under the graph of from to and above the -axis, using four rectangles. Let the height of each rectangle be the function value at the midpoint of the interval.
(Short Answer)
4.7/5  (33)
(33)
find the value of the given limit if it exists. If the function approaches or , say so.
-
(Short Answer)
4.8/5  (37)
(37)
Showing 61 - 80 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)