Exam 4: Rational, Power, and Root Functions
Exam 1: Linear Functions, Equations, and Inequalities44 Questions
Exam 2: Analysis of Graphs of Functions84 Questions
Exam 3: Polynomial Functions40 Questions
Exam 4: Rational, Power, and Root Functions48 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions84 Questions
Exam 6: Systems and Matrices68 Questions
Exam 7: Analytic Geometry and Nonlinear Systems48 Questions
Exam 8: The Unit Circle and Functions of Trigonometry88 Questions
Exam 9: Trigonometric Identities and Equations100 Questions
Exam 10: Applications of Trigonometry and Vectors40 Questions
Exam 11: Further Topics in Algebra48 Questions
Exam 12: Limits, Derivatives, and Definite Integrals100 Questions
Exam 13: Reference: Basic Algebraic Concepts40 Questions
Select questions type
(a) Sketch the graph of .
(b) Explain how the graph in part (a) is obtained from the graph of .
(c) Use a graphing calculator to obtain an accurate depiction of the graph in part (a).
(Essay)
4.9/5  (45)
(45)
Consider the rational function defined by . Determine the answers to (a) - (e) analytically:
(a) Equations of the vertical asymptotes
(b) Equation of the horizontal asymptote
(c) -intercept
(d) -intercepts, if any
(e) Coordinates of the point where the graph of intersects its horizontal asymptote. Now sketch a comprehensive graph of .
(Essay)
4.8/5  (38)
(38)
(a) Solve the following rational equation analytically: .
(b) Use the results of part (a) and a graph to find the solution set of .
(Short Answer)
4.9/5  (35)
(35)
Graph the function in the standard viewing window. Then do each of the following:
(a) Determine the domain analytically.
(b) Use the graph to find the range.
(c) Fill in the blank with either increases or decreases: The function over its entire domain.
(d) Solve the equation graphically.
(e) Solve the inequality graphically.
(Essay)
4.9/5  (33)
(33)
(a) Sketch the graph of .
(b) Explain how the graph in part (a) is obtained from the graph of .
(c) Use a graphing calculator to obtain an accurate depiction of the graph in part (a).
(Essay)
4.8/5  (39)
(39)
(a) Sketch the graph of .
(b) Explain how the graph in part (a) is obtained from the graph of .
(c) Use a graphing calculator to obtain an accurate depiction of the graph in part (a).
(Essay)
4.9/5  (41)
(41)
A sidewalk in a public park is to be constructed from a restroom at point to the street at point , and another sidewalk is to be constructed from point to a swimming pool at point . Distances are shown in the figure provided. Find the distance which will minimize the combined length of the two sidewalks. What is the total length of the sidewalk to be constructed?
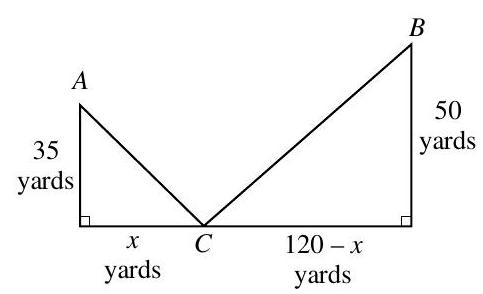
(Short Answer)
4.7/5  (42)
(42)
A building requires a beam 52 meters long, .28 meter wide, and .11 meter high. The maximum load of a horizontal beam that is supported at both ends varies directly as the width and the square of the height and inversely as the length between supports. If a beam of the same material 46 meters long, .30 meter wide, and .08 meter high can support a maximum load of 49.46 kilograms, what is the maximum load the beam in the building will support?
(Short Answer)
4.8/5  (36)
(36)
A sidewalk in a public park is to be constructed from a restroom at point to the street at point , and another sidewalk is to be constructed from point to a swimming pool at point . Distances are shown in the figure provided. Find the distance which will minimize the combined length of the two sidewalks. What is the total length of the sidewalk to be constructed?
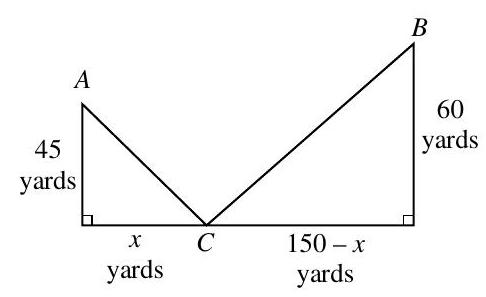
(Short Answer)
4.8/5  (43)
(43)
(a) Solve the equation analytically. Support the solution(s) with a graph.
(b) Use the graph to find the solution set of .
(c) Use the graph to find the solution set of .
(Essay)
4.8/5  (40)
(40)
The parking attendants working at the exit of a parking ramp can process at most 22 cars per minute. If cars arrive randomly at an average rate of vehicles per minute, then the average wait in minutes for a car to exit the ramp is approximated by , where .
(a) Evaluate , and . Interpret the results.
(b) Graph using the window by . Identify the vertical asymptote. What happens to as approaches 22?
(c) Find when the wait is 5 minutes.
(Essay)
4.9/5  (32)
(32)
A manufacturer needs to construct a box with a lid for a special product. The only stipulations are that the volume of the box should be 1500 cubic centimeters and that the box should have a square base. The cost for producing such a box has been determined to be represented by the function , where is the cost of the box in dollars and is the length of a side of the base in centimeters. Use the graph of to determine the side length that will minimize the cost of the box, and determine what this cost will be.
(Hint: Use the window by .)
(Essay)
4.9/5  (33)
(33)
Consider the rational function defined by .
(a) For what value of does the graph exhibit a "hole"?
(b) Graph the function and show the "hole" in the graph.
(Essay)
4.9/5  (36)
(36)
(a) Solve the following rational equation analytically: .
(b) Use the results of part (a) and a graph to find the solution set of .
(Short Answer)
4.9/5  (41)
(41)
The concession stand at a sporting event can fill at most 9 orders per minute. If people arrive randomly at an average rate of people per minute, then the average wait in minutes before an order is filled is approximated by , where .
(a) Evaluate , and . Interpret the results.
(b) Graph using the window by . Identify the vertical asymptote. What happens to as approaches 9 ?
(c) Find when the wait is 2 minutes.
(Essay)
4.8/5  (42)
(42)
Find the equation of the oblique asymptote of the graph of the rational function defined by . Then graph the function and its asymptote using a graphing calculator to illustrate an accurate comprehensive graph.
(Essay)
4.8/5  (32)
(32)
Two buildings are situated on level ground, 65 feet apart, as shown in the figure. The building on the left is 20 feet high and the other building is 40 feet high. An expensive decorative banner is to be strung from the top edge of one building to the top edge of the other, pulled tightly so that it touches the ground at point somewhere between the two buildings. Let represent the distance from to the base of the building on the left. Find the value of that will minimize the length of the banner. How long is this banner?
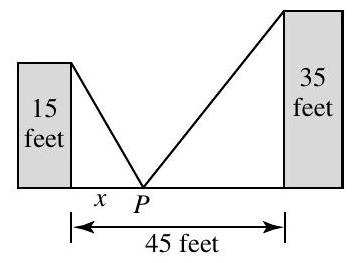
(Short Answer)
4.9/5  (45)
(45)
A building requires a beam 44 meters long, .32 meter wide, and .12 meter high. The maximum load of a horizontal beam that is supported at both ends varies directly as the width and the square of the height and inversely as the length between supports. If a beam of the same material 38 meter long, .25 meter wide, and .11 meter high can support a maximum load of 94.33 kilograms, what is the maximum load the beam in the building will support?
(Short Answer)
4.9/5  (44)
(44)
The length and cross-sectional area of a wire determine the resistance that the wire gives to the flow of electricity. The resistance of a wire varies directly as the length of the wire and inversely as the cross-sectional area. A wire with a length of and a cross-sectional area of has a resistance of . If another wire has a length of and a cross-sectional area of , determine the resistance of the wire.
(Short Answer)
4.9/5  (29)
(29)
Graph the function in the standard viewing window. Then do each of the following:
(a) Determine the domain analytically.
(b) Use the graph to find the range.
(c) Fill in the blank with either increases or decreases: The function over its entire domain.
(d) Solve the equation graphically.
(e) Solve the inequality graphically.
(Essay)
4.8/5  (43)
(43)
Showing 21 - 40 of 48
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)