Exam 1: Linear Functions, Equations, and Inequalities
Exam 1: Linear Functions, Equations, and Inequalities44 Questions
Exam 2: Analysis of Graphs of Functions84 Questions
Exam 3: Polynomial Functions40 Questions
Exam 4: Rational, Power, and Root Functions48 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions84 Questions
Exam 6: Systems and Matrices68 Questions
Exam 7: Analytic Geometry and Nonlinear Systems48 Questions
Exam 8: The Unit Circle and Functions of Trigonometry88 Questions
Exam 9: Trigonometric Identities and Equations100 Questions
Exam 10: Applications of Trigonometry and Vectors40 Questions
Exam 11: Further Topics in Algebra48 Questions
Exam 12: Limits, Derivatives, and Definite Integrals100 Questions
Exam 13: Reference: Basic Algebraic Concepts40 Questions
Select questions type
Suppose that an empty circular wading pool has a radius of 5 feet. During a storm, rain falling at a rate of 1.5 inches per hour begins to fill the pool. A small drain at the bottom of the pool is capable of draining 30 gallons of water per hour.
(a) Determine the number of cubic inches of water falling into the pool in one hour. (Hint: Each hour a layer of water 1.5 inches thick falls into the pool.)
(b) One gallon of water equals about 231 cubic inches. Write a formula for a function that computes the gallons of water landing in the pool in hours.
(c) How many gallons of water land in the pool during a 2.5 hour storm?
(d) Will the drain be able to keep up with the rainfall? If not, how many such drains would be needed?
(Essay)
4.8/5  (37)
(37)
Suppose that an empty circular wading pool has a radius of 5 feet. During a storm, rain falling at a rate of 0.6 inch per hour begins to fill the pool. A small drain at the bottom of the pool is capable of draining 35 gallons of water per hour.
(a) Determine the number of cubic inches of water falling into the pool in one hour. (Hint: Each hour a layer of water 0.6 inch thick falls into the pool.)
(b) One gallon of water equals about 231 cubic inches. Write a formula for a function that computes the gallons of water landing in the pool in hours.
(c) How many gallons of water land in the pool during a 2 hour storm?
(d) Will the drain be able to keep up with the rainfall? If not, how many such drains would be needed?
(Essay)
4.9/5  (40)
(40)
Find the equation of the line passing through the point and
(a) parallel to the line with equation .
(b) perpendicular to the line with equation .
(Essay)
4.8/5  (29)
(29)
Use the screen to solve the equation or inequality. Here the function is a linear function defined over the domain of real numbers.
(a)
(b)
(c)
(d)
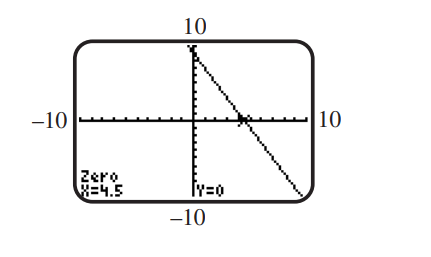
(Essay)
4.9/5  (39)
(39)
Find the - and -intercepts of the line whose standard form is . What is the slope of this line?
(Essay)
4.9/5  (35)
(35)
For each of the functions, determine the
(i) domain
(ii) range
(iii) x-intercept(s)
(iv) y-intercept(s).
(a) 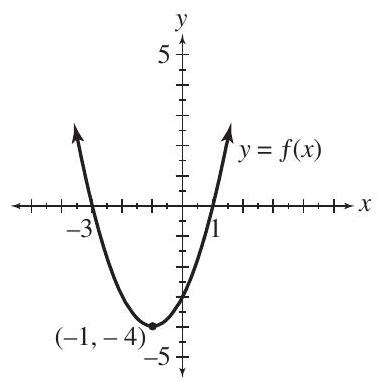 (b)
(b) 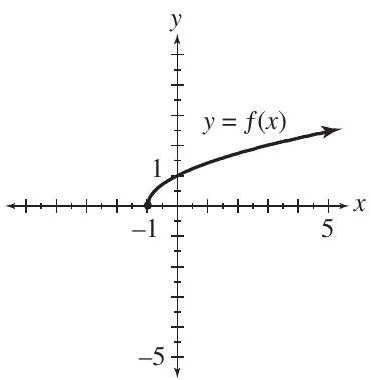 (c)
(c) 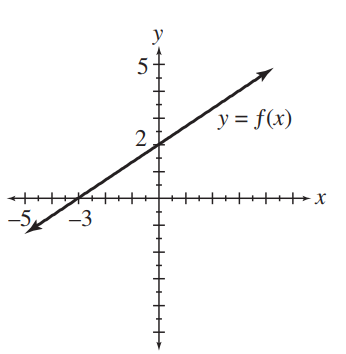
(Essay)
4.8/5  (32)
(32)
Consider the linear functions and .
(a) Solve analytically, showing all steps. Also, check analytically.
(b) Graph and and use your result in part (a) to find the solution set of . Explain your answer.
(c) Repeat part (b) for
(Essay)
4.8/5  (35)
(35)
Find the - and -intercepts of the line whose standard form is .
What is the slope of this line?
(Essay)
4.9/5  (32)
(32)
Suppose that an empty circular wading pool has a radius of 9 feet. During a storm, rain falling at a rate of 0.5 inch per hour begins to fill the pool. A small drain at the bottom of the pool is capable of draining 20 gallons of water per hour.
(a) Determine the number of cubic inches of water falling into the pool in one hour. (Hint: Each hour a layer of water 0.5 inch thick falls into the pool.)
(b) One gallon of water equals about 231 cubic inches. Write a formula for a function that computes the gallons of water landing in the pool in hours.
(c) How many gallons of water land in the pool during a 2.5 hour storm?
(d) Will the drain be able to keep up with the rainfall? If not, how many such drains would be needed?
(Essay)
4.7/5  (43)
(43)
Consider the linear function .
(a) Solve the equation analytically.
(b) Solve the inequality analytically.
(c) Graph in an appropriate viewing window and explain how the graph supports your answers in parts (a) and (b).
(Essay)
4.7/5  (41)
(41)
Consider the linear function .
(a) Solve the equation analytically.
(b) Solve the inequality analytically.
(c) Graph in an appropriate viewing window and explain how the graph supports your answers in parts (a) and (b).
(Essay)
4.9/5  (21)
(21)
The graph below shows a line segment depicting the number of injuries and illnesses resulting in days away from work from 2004 to 2006. (Source: U.S. Department of Labor Statistics)
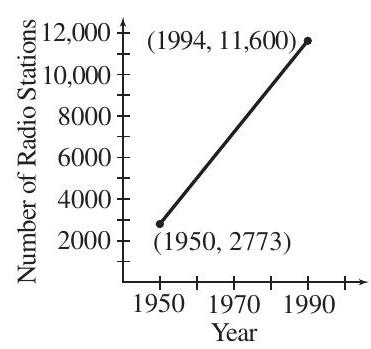 (a) Use the midpoint formula to approximate the number of illnesses and injuries during the year 2005.
(b) Find the slope of the line and explain its meaning in the context of this situation.
(a) Use the midpoint formula to approximate the number of illnesses and injuries during the year 2005.
(b) Find the slope of the line and explain its meaning in the context of this situation.
(Essay)
4.8/5  (38)
(38)
For each of the functions, determine the
(i) domain
(ii) range
(iii) -intercept(s)
(iv) -intercept(s).
(a)
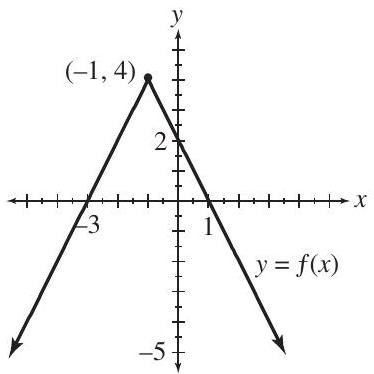 (b)
(b)
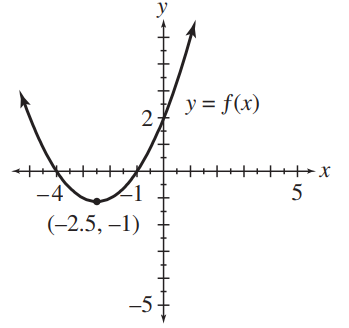 (c)
(c)
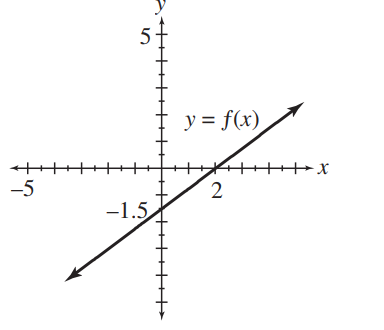
(Essay)
4.7/5  (30)
(30)
Use the screen to solve the equation or inequality. Here the function is a linear function defined over the domain of real numbers.
(a)
(b)
(c)
(d)
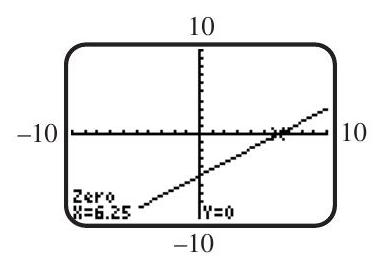
(Essay)
4.8/5  (39)
(39)
Consider the linear functions and .
(a) Solve analytically, showing all steps. Also, check analytically.
(b) Graph and and use your result in part (a) to find the solution set of . Explain your answer.
(c) Repeat part (b) for
(Essay)
4.9/5  (32)
(32)
Consider the linear functions and .
(a) Solve analytically, showing all steps. Also, check analytically.
(b) Graph and and use your result in part (a) to find the solution set of . Explain your answer.
(c) Repeat part (b) for .
(Essay)
4.9/5  (38)
(38)
Use the screen to solve the equation or inequality. Here the function is a linear function defined over the domain of real numbers.
(a)
(b)
(c)
(d)
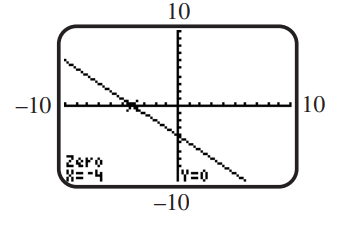
(Essay)
4.7/5  (27)
(27)
Showing 21 - 40 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)