Question 1

Determine whether the given quadratic function has a maximum or minimum value. Then find that maximum or minimum value.
-$f(x)=4 x^{2}-8 x+8$

Accepted Answer

A)  Minimum, 4 
B)  Maximum, 4 
C)  Maximum, 1 
D)  Minimum, 1 
A)  Minimum, 4 
B)  Maximum, 4 
C)  Maximum, 1 
D)  Minimum, 1

Question 2

Solve by using the quadratic formula
-$x^{2}+72=18 x$

Accepted Answer

A)  $\{12,6\}$ 
B)  $\{-12,-6\}$ 
C)  $\{-72,-1\}$ 
D)  $\{1,72\}$ 
A)  $\{12,6\}$ 
B)  $\{-12,-6\}$ 
C)  $\{-72,-1\}$ 
D)  $\{1,72\}$

Question 3

Determine a quadratic function that results when applying the given shifts to the graph of $f(x)=x^{2}$.
-Shift 20 units up.

Accepted Answer

A)  $f(x)=(x-20)^{2}$ 
B)  $f(x)=(x+20)^{2}$ 
C)  $f(x)=x^{2}+20$ 
D)  $f(x)=x^{2}-20$ 
A)  $f(x)=(x-20)^{2}$ 
B)  $f(x)=(x+20)^{2}$ 
C)  $f(x)=x^{2}+20$ 
D)  $f(x)=x^{2}-20$

Question 4

Solve by using the quadratic formula
-$x^{2}+x+6=0$

Accepted Answer

A)  $\left\{\frac{-1 \pm \sqrt{23}}{2}\right\}$ 
B)  $\left\{\frac{1 \pm \sqrt{23} \mathrm{i}}{2}\right\}$ 
C)  $\left\{\frac{-1 \pm \sqrt{23} \mathrm{i}}{2}\right\}$ 
D)  $\left\{\frac{1 \pm \sqrt{23}}{2}\right\}$ 
A)  $\left\{\frac{-1 \pm \sqrt{23}}{2}\right\}$ 
B)  $\left\{\frac{1 \pm \sqrt{23} \mathrm{i}}{2}\right\}$ 
C)  $\left\{\frac{-1 \pm \sqrt{23} \mathrm{i}}{2}\right\}$ 
D)  $\left\{\frac{1 \pm \sqrt{23}}{2}\right\}$

Question 5

Find the term that should be added to the expression to form a perfect square trinomial. Write the resulting perfect square trinomial in factored form.
-$x^{2}-2 x$

Accepted Answer

A)  $1 ;(x+1)^{2}$ 
B)  $1 ;(x-2)^{2}$ 
C)  $0 ;(x-1)^{2}$ 
D)  $1 ;(x-1,)^{2}$ 
A)  $1 ;(x+1)^{2}$ 
B)  $1 ;(x-2)^{2}$ 
C)  $0 ;(x-1)^{2}$ 
D)  $1 ;(x-1,)^{2}$

Question 6

Use the table below for values of $\cos (\theta)$ and $\sin (\theta)$.
$\begin{array}{|c|l|l|}
\hline \theta(\text { degrees }) & \cos (\boldsymbol{\theta}) & \sin (\boldsymbol{\theta}) \
\hline 10 & 0.985 & 0.174 \
\hline 20 & 0.940 & 0.342 \
\hline 30 & 0.866 & 0.500 \
\hline 40 & 0.766 & 0.643 \
\hline 45 & 0.707 & 0.707 \
\hline 50 & 0.643 & 0.766 \
\hline 60 & 0.500 & 0.866 \
\hline 70 & 0.342 & 0.940 \
\hline 80 & 0.174 & 0.985 \
\hline
\end{array}$

A projectile is launched with an initial velocity of $150 \mathrm{ft} / \mathrm{s}$ from a height of 30 feet above the ground.
a) Complete the table by filling in the time required for the projectile to land. Round to the nearest hundredth of a second.
$\begin{array}{|l|l|}
\hline \boldsymbol{\theta} \text { (degrees) } & \text { Time }(s) \
\hline 10 & \
\hline 30 & \
\hline 50 & \
\hline 70 & \
\hline
\end{array}$

b) What launch angle gives the projectile the longest time in the air?
c) Complete the table by filling in the distance traveled horizontally by the projectile. Use the times found in part a. Round to the nearest hundredth of a foot.
$\begin{array}{|l|l|}
\hline \boldsymbol{\theta} \text { (degrees) } & \text { Distance }(\text { ft }) \
\hline
\end{array}$

d) What launch angle gives the greatest horizontal distance?

Accepted Answer

A) 
a)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 3.72 \
\hline 30 & 6.19 \
\hline 50 & 8.93 \
\hline 70 & 9.41 \
\hline
\end{array}$
b)$70^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 411.87 \
\hline 30 & 698.63 \
\hline 50 & 571.08 \
\hline 70 & 493.77\
\hline 
\end{array}$
d)$30^\circ$ 
B) 
a)$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 10.86 \
\hline 30 & 8.64 \
\hline 50 & 7.43 \
\hline 70 & 5.83 \
\hline
\end{array}$
b)$10^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 676.55 \
\hline 30 & 732.71 \
\hline 50 & 786.62 \
\hline 70 & 825.83 \
\hline
\end{array}$
d)$70^\circ$ 
C) 
a)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 1.68 \
\hline 30 & 3.81 \
\hline 50 & 3.96 \
\hline 70 & 1.95\
\hline
\end{array}$
b)$50^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 683.07 \
\hline 30 & 521.65 \
\hline 50 & 519.96 \
\hline 70 & 417.38 \
\hline
\end{array}$
d)$10^\circ$ 
D) 
a)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 2.41 \
\hline 30 & 5.06 \
\hline 50 & 7.43 \
\hline 70 & 9.02 \
\hline
\end{array}$
b)$70^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 356.08 \
\hline 30 & 657.29 \
\hline 50 & 716.62 \
\hline 70 & 462.73 \
\hline
\end{array}$
d)$50^circ$ 
A) 
a)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 3.72 \
\hline 30 & 6.19 \
\hline 50 & 8.93 \
\hline 70 & 9.41 \
\hline
\end{array}$
b)$70^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 411.87 \
\hline 30 & 698.63 \
\hline 50 & 571.08 \
\hline 70 & 493.77\
\hline 
\end{array}$
d)$30^\circ$ 
B) 
a)$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 10.86 \
\hline 30 & 8.64 \
\hline 50 & 7.43 \
\hline 70 & 5.83 \
\hline
\end{array}$
b)$10^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 676.55 \
\hline 30 & 732.71 \
\hline 50 & 786.62 \
\hline 70 & 825.83 \
\hline
\end{array}$
d)$70^\circ$ 
C) 
a)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 1.68 \
\hline 30 & 3.81 \
\hline 50 & 3.96 \
\hline 70 & 1.95\
\hline
\end{array}$
b)$50^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 683.07 \
\hline 30 & 521.65 \
\hline 50 & 519.96 \
\hline 70 & 417.38 \
\hline
\end{array}$
d)$10^\circ$ 
D) 
a)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Time }(\mathbf{s}) \
\hline 10 & 2.41 \
\hline 30 & 5.06 \
\hline 50 & 7.43 \
\hline 70 & 9.02 \
\hline
\end{array}$
b)$70^\circ$
c)
$\begin{array}{|l|l|}
\hline \theta \text { (degrees) } & \text { Distance }(\mathrm{ft}) \
\hline 10 & 356.08 \
\hline 30 & 657.29 \
\hline 50 & 716.62 \
\hline 70 & 462.73 \
\hline
\end{array}$
d)$50^circ$

Question 7

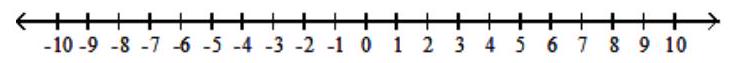
Solve the quadratic inequality. Express your solution on a number line using interval notation.
-$(\mathrm{x}-5)(\mathrm{x}+7)>0$

Accepted Answer

A)  $ (-\infty,-7) \cup(5, \infty) $
  
B)  $ (-\infty,-5) \cup(7, \infty) $
  
C)  $ (-7,5) $
  
D)  $ (-7, \infty) $
  
A)  $ (-\infty,-7) \cup(5, \infty) $
  
B)  $ (-\infty,-5) \cup(7, \infty) $
  
C)  $ (-7,5) $
  
D)  $ (-7, \infty) $

Question 8

Without graphing the function, state the shift(s) that are applied to the graph of $f(x)=x^{2}$ to graph the given function. If the graph of $f(x)=x^{2}$ must be rotated about the $x$-axis, state this.
-$f(x)=(x-4)^{2}-6$

Accepted Answer

A)  right 6 units, down 4 units 
B)  left 4 units, down 6 units 
C)  right 4 units, down 6 units 
D)  left 6 units, down 4 units 
A)  right 6 units, down 4 units 
B)  left 4 units, down 6 units 
C)  right 4 units, down 6 units 
D)  left 6 units, down 4 units

Question 9

Find the $x$ - and $y$-intercepts of the parabola associated with the quadratic equation. If the parabola does not have any $x$-intercepts, state "no $x$-intercepts."
-$y=2 x^{2}+12 x+16$

Accepted Answer

A)  $(-4,0),(-2,0),(0,16)$ 
B)  $(4,0),(2,0),(0,16)$ 
C)  $(4,0),(-2,0),(0,-16)$ 
D)  $(-4,0),(2,0),(0,-16)$ 
A)  $(-4,0),(-2,0),(0,16)$ 
B)  $(4,0),(2,0),(0,16)$ 
C)  $(4,0),(-2,0),(0,-16)$ 
D)  $(-4,0),(2,0),(0,-16)$

Question 10

Solve by using the quadratic formula
-$2 x^{2}+10 x=-4$

Accepted Answer

A)  $\left\{\frac{-10 \pm \sqrt{17}}{2}\right\}$ 
B)  $\left\{\frac{-5 \pm \sqrt{33}}{2}\right\}$ 
C)  $\left\{\frac{-5 \pm \sqrt{17}}{2}\right\}$ 
D)  $\left\{\frac{-5 \pm \sqrt{17}}{4}\right\}$ 
A)  $\left\{\frac{-10 \pm \sqrt{17}}{2}\right\}$ 
B)  $\left\{\frac{-5 \pm \sqrt{33}}{2}\right\}$ 
C)  $\left\{\frac{-5 \pm \sqrt{17}}{2}\right\}$ 
D)  $\left\{\frac{-5 \pm \sqrt{17}}{4}\right\}$

Question 11

Solve by extracting square roots
-$(x+16)^{2}-6=0$

Accepted Answer

A)  $\{4 \pm \sqrt{6}\}$ 
B)  $\{16 \pm \sqrt{6}\}$ 
C)  $\{-16 \pm \mathrm{i} \sqrt{6}\}$ 
D)  $\{10,22\}$ 
A)  $\{4 \pm \sqrt{6}\}$ 
B)  $\{16 \pm \sqrt{6}\}$ 
C)  $\{-16 \pm \mathrm{i} \sqrt{6}\}$ 
D)  $\{10,22\}$

Question 12

Determine a quadratic function that results when applying the given shifts to the graph of $f(x)=x^{2}$.
-Rotate about the $x$ - axis, shift 2 units to the left and 4 units down.

Accepted Answer

A)  $f(x)=-(x-4)^{2}+2$ 
B)  $f(x)=(-x+2)^{2}-4$ 
C)  $f(x)=-(x-2)^{2}-4$ 
D)  $f(x)=-(x+2)^{2}-4$ 
A)  $f(x)=-(x-4)^{2}+2$ 
B)  $f(x)=(-x+2)^{2}-4$ 
C)  $f(x)=-(x-2)^{2}-4$ 
D)  $f(x)=-(x+2)^{2}-4$

Question 13

Find the vertex of the parabola associated with the quadratic equation.
-$y=x^{2}+2 x+8$

Accepted Answer

A)  $(1,8)$ 
B)  $(-1,7)$ 
C)  $(-1,8)$ 
D)  $(1,7)$ 
A)  $(1,8)$ 
B)  $(-1,7)$ 
C)  $(-1,8)$ 
D)  $(1,7)$

Question 14

State the domain and range of the given function
-$f(x)=(x-7)^{2}$

Accepted Answer

A)  Domain: $(-\infty, \infty)$ Range: $[-7, \infty)$ 
B)  Domain: $(-\infty, \infty)$ Range: $(-\infty, \infty)$ 
C)  Domain: $(-\infty, \infty)$ Range: $[0, \infty)$ 
D)  Domain: $[7, \infty)$ Range: $(-\infty, \infty)$ 
A)  Domain: $(-\infty, \infty)$ Range: $[-7, \infty)$ 
B)  Domain: $(-\infty, \infty)$ Range: $(-\infty, \infty)$ 
C)  Domain: $(-\infty, \infty)$ Range: $[0, \infty)$ 
D)  Domain: $[7, \infty)$ Range: $(-\infty, \infty)$

Question 15

Find the vertex of the parabola associated with the quadratic equation.
-$y=x^{2}+2 x-3$

Accepted Answer

A)  $(1,-4)$ 
B)  $(-1,-4)$ 
C)  $(1,4)$ 
D)  $(-1,-3)$ 
A)  $(1,-4)$ 
B)  $(-1,-4)$ 
C)  $(1,4)$ 
D)  $(-1,-3)$

Question 16

Find a rational inequality whose solution is given
-

Accepted Answer

A)  $\frac{x^{2}-11 x+18}{x^{2}-4 x-21}>0$ 
B)  $\frac{x^{2}-11 x+18}{x^{2}-4 x-21} \leq 0$ 
C)  $\frac{x^{2}-4 x-21}{x^{2}-11 x+18} \leq 0$ 
D)  $\frac{x^{2}-11 x+18}{x^{2}-4 x-21} \geq 0$ 
A)  $\frac{x^{2}-11 x+18}{x^{2}-4 x-21}>0$ 
B)  $\frac{x^{2}-11 x+18}{x^{2}-4 x-21} \leq 0$ 
C)  $\frac{x^{2}-4 x-21}{x^{2}-11 x+18} \leq 0$ 
D)  $\frac{x^{2}-11 x+18}{x^{2}-4 x-21} \geq 0$

Question 17

Graph the function, and state its domain and range
-$ f(x)=\sqrt{x-4} $

Accepted Answer

A)  Domain: $ [-4, \infty) $; Range: $ [0, \infty) $
  
B)  Domain: $ [0, \infty) $; Range: $ [-4, \infty) $
  
C)  Domain: $ [4, \infty) $; Range: $ [0, \infty) $
  
D)  Domain: $ [0, \infty) $; Range: $ [4, \infty) $
  
A)  Domain: $ [-4, \infty) $; Range: $ [0, \infty) $
  
B)  Domain: $ [0, \infty) $; Range: $ [-4, \infty) $
  
C)  Domain: $ [4, \infty) $; Range: $ [0, \infty) $
  
D)  Domain: $ [0, \infty) $; Range: $ [4, \infty) $

Question 18

Find a quadratic inequality whose solution is given.
-

Accepted Answer

A)  $x^{2}+100 \leq 0$ 
B)  $x^{2}+100 \geq 0$ 
C)  $x^{2}-100 \leq 0$ 
D)  $x^{2}-100 \geq 0$ 
A)  $x^{2}+100 \leq 0$ 
B)  $x^{2}+100 \geq 0$ 
C)  $x^{2}-100 \leq 0$ 
D)  $x^{2}-100 \geq 0$

Question 19

State the domain and range of the given function
-$f(x)=x^{2}-3$

Accepted Answer

A)  Domain: $(-\infty, \infty)$
Range: $(-\infty, \infty)$ 
B)  Domain: $[-3, \infty)$
Range: $(-\infty, \infty)$ 
C)  Domain: $(-\infty, \infty)$
Range: $[3, \infty)$ 
D)  Domain: $(-\infty, \infty)$
Range: $[-3, \infty)$ 
A)  Domain: $(-\infty, \infty)$
Range: $(-\infty, \infty)$ 
B)  Domain: $[-3, \infty)$
Range: $(-\infty, \infty)$ 
C)  Domain: $(-\infty, \infty)$
Range: $[3, \infty)$ 
D)  Domain: $(-\infty, \infty)$
Range: $[-3, \infty)$

Question 20

Find the $x$ - and $y$-intercepts. If no $x$-intercepts exist, state so.
-$f(x)=-x^{2}+9 x-20$

Accepted Answer

A)  $(4,0),(5,0),(0,-20)$ 
B)  No $x$-intercepts, $(0,4)$ 
C)  $(-4,0),(-5,0),(0,-20)$ 
D)  $(4,0),(5,0),(0,4)$ 
A)  $(4,0),(5,0),(0,-20)$ 
B)  No $x$-intercepts, $(0,4)$ 
C)  $(-4,0),(-5,0),(0,-20)$ 
D)  $(4,0),(5,0),(0,4)$

Determine whether the given quadratic function has a maximum or minimum value. Then find that maximum or minimum value. - $f(x)=4 x^{2}-8 x+8$

Solve by using the quadratic formula - $x^{2}+72=18 x$

Determine a quadratic function that results when applying the given shifts to the graph of $f(x)=x^{2}$ . -Shift 20 units up.

Solve by using the quadratic formula - $x^{2}+x+6=0$

Find the term that should be added to the expression to form a perfect square trinomial. Write the resulting perfect square trinomial in factored form. - $x^{2}-2 x$

Solve the quadratic inequality. Express your solution on a number line using interval notation. - $(\mathrm{x}-5)(\mathrm{x}+7)>0$ $Solve the quadratic inequality. Express your solution on a number line using interval notation. - (\mathrm{x}-5)(\mathrm{x}+7)>0$

Without graphing the function, state the shift(s) that are applied to the graph of $f(x)=x^{2}$ to graph the given function. If the graph of $f(x)=x^{2}$ must be rotated about the $x$ -axis, state this. - $f(x)=(x-4)^{2}-6$

Find the $x$ - and $y$ -intercepts of the parabola associated with the quadratic equation. If the parabola does not have any $x$ -intercepts, state "no $x$ -intercepts." - $y=2 x^{2}+12 x+16$

Solve by using the quadratic formula - $2 x^{2}+10 x=-4$

Solve by extracting square roots - $(x+16)^{2}-6=0$

Determine a quadratic function that results when applying the given shifts to the graph of $f(x)=x^{2}$ . -Rotate about the $x$ - axis, shift 2 units to the left and 4 units down.

Find the vertex of the parabola associated with the quadratic equation. - $y=x^{2}+2 x+8$

State the domain and range of the given function - $f(x)=(x-7)^{2}$

Find the vertex of the parabola associated with the quadratic equation. - $y=x^{2}+2 x-3$

Find a rational inequality whose solution is given -

Graph the function, and state its domain and range - $f(x)=\sqrt{x-4}$ $Graph the function, and state its domain and range - f(x)=\sqrt{x-4}$

Find a quadratic inequality whose solution is given. -

State the domain and range of the given function - $f(x)=x^{2}-3$

Find the $x$ - and $y$ -intercepts. If no $x$ -intercepts exist, state so. - $f(x)=-x^{2}+9 x-20$

Review of Real Numbers

Linear and Absolute Value Equations and Inequalities

Graphing Linear Equations

Systems of Equations

Exponents, Polynomials, and Factoring Polynomials

Rational Expressions and Equations

Radical Expressions and Equations

Logarithmic and Exponential Functions

Conic Sections

Sequences, Series, and the Binomial Theorem

Filters

Exam 8: Quadratic Equations

Determine whether the given quadratic function has a maximum or minimum value. Then find that maximum or minimum value. - f(x)=4x2−8x+8f(x)=4 x^{2}-8 x+8f(x)=4x2−8x+8

Solve by using the quadratic formula - x2+72=18xx^{2}+72=18 xx2+72=18x

Determine a quadratic function that results when applying the given shifts to the graph of f(x)=x2f(x)=x^{2}f(x)=x2 . -Shift 20 units up.

Solve by using the quadratic formula - x2+x+6=0x^{2}+x+6=0x2+x+6=0

Find the term that should be added to the expression to form a perfect square trinomial. Write the resulting perfect square trinomial in factored form. - x2−2xx^{2}-2 xx2−2x

Solve the quadratic inequality. Express your solution on a number line using interval notation. - (x−5)(x+7)>0(\mathrm{x}-5)(\mathrm{x}+7)>0(x−5)(x+7)>0

Without graphing the function, state the shift(s) that are applied to the graph of f(x)=x2f(x)=x^{2}f(x)=x2 to graph the given function. If the graph of f(x)=x2f(x)=x^{2}f(x)=x2 must be rotated about the xxx -axis, state this. - f(x)=(x−4)2−6f(x)=(x-4)^{2}-6f(x)=(x−4)2−6

Find the xxx - and yyy -intercepts of the parabola associated with the quadratic equation. If the parabola does not have any xxx -intercepts, state "no xxx -intercepts." - y=2x2+12x+16y=2 x^{2}+12 x+16y=2x2+12x+16

Solve by using the quadratic formula - 2x2+10x=−42 x^{2}+10 x=-42x2+10x=−4

Solve by extracting square roots - (x+16)2−6=0(x+16)^{2}-6=0(x+16)2−6=0

Determine a quadratic function that results when applying the given shifts to the graph of f(x)=x2f(x)=x^{2}f(x)=x2 . -Rotate about the xxx - axis, shift 2 units to the left and 4 units down.

Find the vertex of the parabola associated with the quadratic equation. - y=x2+2x+8y=x^{2}+2 x+8y=x2+2x+8

State the domain and range of the given function - f(x)=(x−7)2f(x)=(x-7)^{2}f(x)=(x−7)2

Find the vertex of the parabola associated with the quadratic equation. - y=x2+2x−3y=x^{2}+2 x-3y=x2+2x−3