Exam 8: Quadratic Equations
Exam 1: Review of Real Numbers152 Questions
Exam 2: Linear and Absolute Value Equations and Inequalities334 Questions
Exam 3: Graphing Linear Equations353 Questions
Exam 4: Systems of Equations204 Questions
Exam 5: Exponents, Polynomials, and Factoring Polynomials453 Questions
Exam 6: Rational Expressions and Equations249 Questions
Exam 7: Radical Expressions and Equations361 Questions
Exam 8: Quadratic Equations270 Questions
Exam 9: Logarithmic and Exponential Functions404 Questions
Exam 10: Conic Sections122 Questions
Exam 11: Sequences, Series, and the Binomial Theorem154 Questions
Select questions type
Determine whether the given quadratic function has a maximum or minimum value. Then find that maximum or minimum value.
-
(Multiple Choice)
4.9/5  (35)
(35)
Solve the quadratic equation using the most efficient technique (factoring, extracting square roots, completing the square, or the quadratic formula).
-
(Multiple Choice)
4.9/5  (36)
(36)
Determine the function that has been graphed. The function will be of the form or . Assume or .
-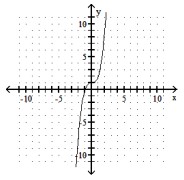
(Multiple Choice)
4.8/5  (29)
(29)
Determine a quadratic function that results when applying the given shifts to the graph of .
-Rotate about the - axis, shift 5 units to the right and 16 units up.
(Multiple Choice)
4.8/5  (36)
(36)
A ladder is resting against a wall. The top of the ladder touches the wall at a height of . Find the length of the ladder if the length is more than its distance from the wall.
(Multiple Choice)
5.0/5  (37)
(37)
Determine whether the given quadratic function has a maximum or minimum value. Then find that maximum or minimum value.
-
(Multiple Choice)
4.9/5  (28)
(28)
Find a quadratic equation with integer coefficients that has the given solution set.
-
(Multiple Choice)
4.8/5  (30)
(30)
Approximate to the nearest tenth when necessary.
-The distance , in feet, that a free- falling object falls in seconds is given by the formula . Find the time that it takes for an object to fall 96 feet.
(Multiple Choice)
4.8/5  (30)
(30)
Solve the quadratic inequality. Express your solution on a number line using interval notation.
-
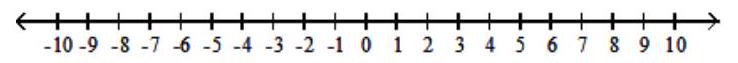
(Multiple Choice)
4.8/5  (38)
(38)
Find the - and -intercepts of the parabola associated with the quadratic equation. If the parabola does not have any -intercepts, state "no -intercepts."
-
(Multiple Choice)
4.8/5  (32)
(32)
Find the - and -intercepts of the parabola associated with the quadratic equation. If the parabola does not have any -intercepts, state "no -intercepts."
-
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the given quadratic function has a maximum or minimum value. Then find that maximum or minimum value.
-
(Multiple Choice)
4.9/5  (39)
(39)
Showing 101 - 120 of 270
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)