Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems
Exam 1: Review of the Real Number System431 Questions
Exam 2: Linear Equations, Inequalities, and Applications338 Questions
Exam 3: Linear Equations, Graphs, and Functions347 Questions
Exam 4: Systems of Linear Equations166 Questions
Exam 5: Exponents, Polynomials, and Polynomial Functions327 Questions
Exam 6: Factoring180 Questions
Exam 7: Rational Expressions and Functions233 Questions
Exam 8: Roots, Radicals, and Root Functions358 Questions
Exam 9: Quadratic Equations, Inequalities, and Functions339 Questions
Exam 10: Inverse, Exponential, and Logarithmic Functions292 Questions
Exam 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems233 Questions
Exam 12: Further Topics in Algebra190 Questions
Exam 13: Appendices29 Questions
Select questions type
Suppose that a nonlinear system is composed of equations whose graphs are those described, and the number of points of intersection of the two graphs is as given. Make a sketch satisfying these conditions.
-Two parabolas; four points
(Essay)
4.8/5  (31)
(31)
The hyperbola shown in the calculator-generated graph was graphed in function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
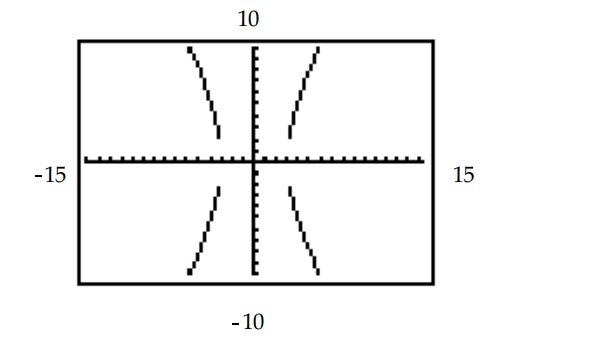
(Multiple Choice)
4.9/5  (36)
(36)
Suppose that a nonlinear system is composed of equations whose graphs are those described, and the number of points of intersection of the two graphs is as given. Make a sketch satisfying these conditions.
-A line and a parabola; one point
(Essay)
4.9/5  (35)
(35)
Solve the problem. Round your answer to the nearest tenth.
-The roof of a building is in the shape of the top half of the hyperbola , where and are in meters. Refer to the figure and determine the height, , of the outside walls.
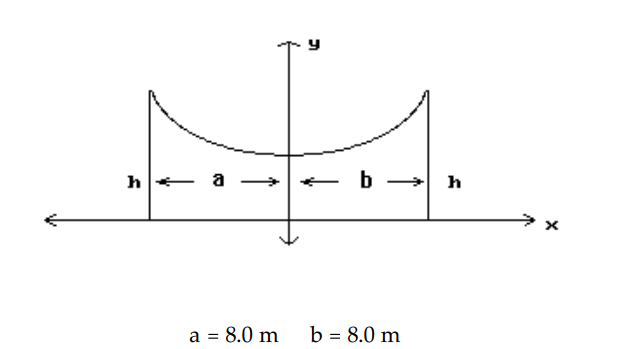
(Multiple Choice)
4.8/5  (34)
(34)
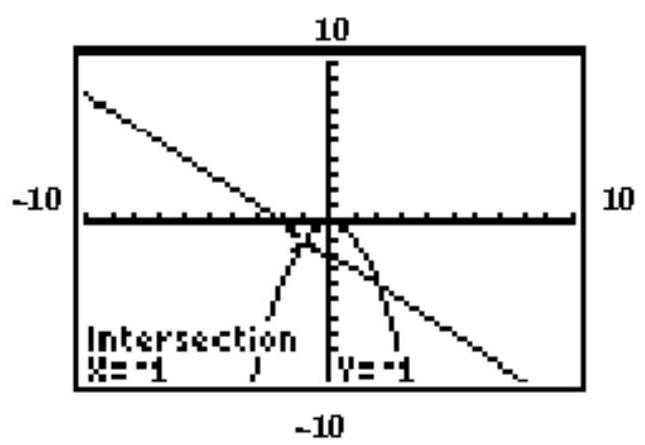
The graphing calculator screen shows the graphs of the two given functions, and the display gives the coordinates of one of the solutions. Find the other solution.
-
(Multiple Choice)
4.9/5  (34)
(34)
Which method should be used to solve the system? Explain your answer, including a description of the first step.
-
(Essay)
4.8/5  (35)
(35)
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
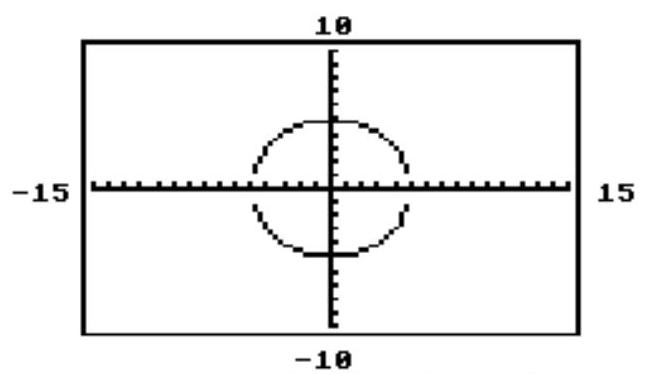
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-A rectangular board is 8 by 20 . How far from the center of the board will the foci be located to determine the largest elliptical tabletop? Round your answer to the nearest tenth.
(Multiple Choice)
4.7/5  (27)
(27)
Suppose that a nonlinear system is composed of equations whose graphs are those described, and the number of points of intersection of the two graphs is as given. Make a sketch satisfying these conditions.
-An ellipse and a hyperbola; four points
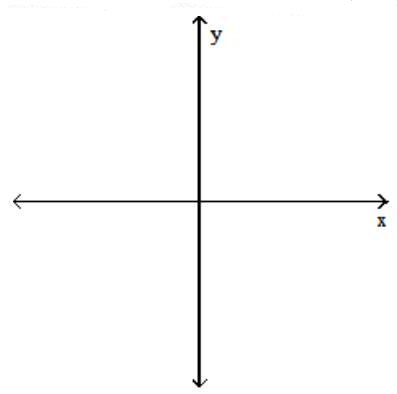
(Essay)
4.9/5  (30)
(30)
Solve the problem.
-A rectangular board is 8 by 14 . The foci of an ellipse are located to produce the largest area. A string is connected to the foci and pulled taut by a pencil in order to draw the ellipse. Find the length of the string.
(Multiple Choice)
4.8/5  (43)
(43)
The hyperbola shown in the calculator-generated graph was graphed in function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
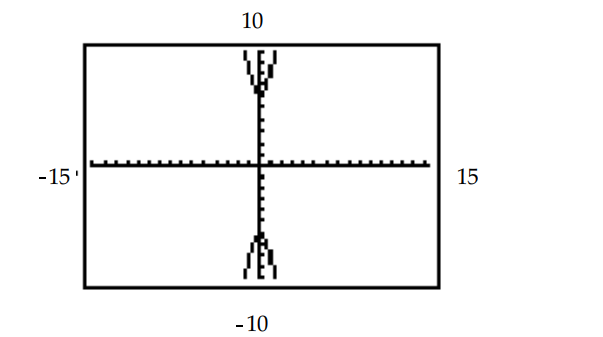
(Multiple Choice)
4.8/5  (34)
(34)
Find the center and radius of the circle whose equation is given.
-
(Multiple Choice)
4.8/5  (35)
(35)
Showing 41 - 60 of 233
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)