Exam 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations
Exam 1: Functions and Their Graphs137 Questions
Exam 2: Polynomial and Rational Functions141 Questions
Exam 3: Exponential and Logarithmic Functions137 Questions
Exam 4: Trigonometric Functions of Angles261 Questions
Exam 5: Trigonometric Functions of Real Numbers151 Questions
Exam 6: Analytic Trigonometry267 Questions
Exam 7: Vectors, the Complex Plane, and Polar Coordinates225 Questions
Exam 8: Systems of Linear Equations and Inequalities181 Questions
Exam 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations230 Questions
Exam 10: Sequences and Series124 Questions
Exam 11: Limits: A Preview to Calculus122 Questions
Exam 12: Review: Equations and Inequalities244 Questions
Select questions type
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
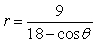
(Short Answer)
4.9/5  (36)
(36)
Graph the second-degree equation. (Hint: Transform the equation into an equation that contains no xy term.)
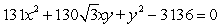
(Short Answer)
4.9/5  (36)
(36)
Find an equation for the parabola with vertex (10, -2) and focus (10, 4).
(Multiple Choice)
4.8/5  (30)
(30)
Graph each equation and find the point(s) of intersection.
X2 + y2 = 26
Y = 5
(Multiple Choice)
4.9/5  (27)
(27)
The given rectangular equation defines a plane curve. Find the parametric equations that also corresponds to the plane curve.
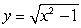
(Short Answer)
4.8/5  (37)
(37)
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
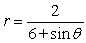
(Short Answer)
4.7/5  (39)
(39)
Identify the conic section given by the following equation as a parabola, ellipse, circle, or hyperbola.
4x2 - 2x + 13y2 - 12y + 20 = 2
(Multiple Choice)
4.8/5  (36)
(36)
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. ,y=t,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a17_a8a5_ad47cfa028f0_TB10663_00.jpg) ,y=t,t in [0, 2π]
,y=t,t in [0, 2π]
(Short Answer)
4.9/5  (35)
(35)
Find an equation for the parabola with focus (9, 3) and directrix y = 9.
(Multiple Choice)
4.8/5  (38)
(38)
Find an equation for the parabola with vertex (2, 10) and focus (10, 10).
(Multiple Choice)
4.8/5  (36)
(36)
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 1]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a19_a8a5_bdf37051c310_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 1]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1a_a8a5_f1c961783a67_TB10663_00.jpg) ,t in [0, 1]
,t in [0, 1]
(Short Answer)
4.8/5  (37)
(37)
Find the polar equation that represents the conic described (assume the focus is at the origin).
Ellipse with eccentricity e =
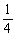 and directrix
and directrix
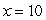
(Short Answer)
4.8/5  (36)
(36)
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
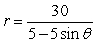
(Short Answer)
4.8/5  (32)
(32)
A satellite dish measures 30 feet across its opening and 13 feet deep at its center. The receiver should be placed at the focus of the parabolic dish. Where is the focus?
(Multiple Choice)
4.9/5  (41)
(41)
Showing 201 - 220 of 230
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)