Exam 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations
Exam 1: Functions and Their Graphs137 Questions
Exam 2: Polynomial and Rational Functions141 Questions
Exam 3: Exponential and Logarithmic Functions137 Questions
Exam 4: Trigonometric Functions of Angles261 Questions
Exam 5: Trigonometric Functions of Real Numbers151 Questions
Exam 6: Analytic Trigonometry267 Questions
Exam 7: Vectors, the Complex Plane, and Polar Coordinates225 Questions
Exam 8: Systems of Linear Equations and Inequalities181 Questions
Exam 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations230 Questions
Exam 10: Sequences and Series124 Questions
Exam 11: Limits: A Preview to Calculus122 Questions
Exam 12: Review: Equations and Inequalities244 Questions
Select questions type
Graph the second-degree equation. (Hint: Transform the equation into an equation that contains no xy term.) 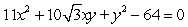
(Multiple Choice)
4.9/5  (32)
(32)
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1c_a8a5_a7145e9d4d96_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1d_a8a5_c5fff45959d3_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
(Short Answer)
4.8/5  (33)
(33)
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a14_a8a5_d53b9504a056_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a15_a8a5_1b57be2bb7b9_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
(Short Answer)
5.0/5  (39)
(39)
Graph each equation and find the point(s) of intersection.
x2 + y = 35
x2 - y = -35
(Short Answer)
5.0/5  (29)
(29)
If the xy-coordinate axes are rotated 60°, find the XY coordinates of the point (x, y) =
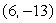 .
.
(Short Answer)
4.8/5  (35)
(35)
Recall that the flight of a projectile can be modeled with the parametric equations:
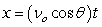 ,
, 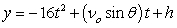 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A missile is fired from a ship at an angle of 31°, an initial height of 13 feet above the water's surface, and at a speed of 5500 feet per second. How long will it be before the missile hits the water? Round to one decimal place.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A missile is fired from a ship at an angle of 31°, an initial height of 13 feet above the water's surface, and at a speed of 5500 feet per second. How long will it be before the missile hits the water? Round to one decimal place.
(Multiple Choice)
4.7/5  (35)
(35)
Graph each equation and find the point(s) of intersection.
X2 + y = 3
X2 - y = -3
(Multiple Choice)
4.8/5  (30)
(30)
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [-π/4,π/4]](https://storage.examlex.com/TB10663/11eed1b2_575d_c132_a8a5_23b1280af6ba_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [-π/4,π/4]](https://storage.examlex.com/TB10663/11eed1b2_575d_c133_a8a5_211dfd65d254_TB10663_00.jpg) ,t in [-π/4,π/4]
,t in [-π/4,π/4]
(Short Answer)
4.8/5  (33)
(33)
A family moves into a new home and decides to fence in the yard to give its dog room to roam. If the area that will be fenced in is rectangular and has an area of 18,723 square feet, and the length is three times as much as the width, how many linear feet of fence should they buy?
(Multiple Choice)
4.9/5  (40)
(40)
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
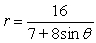
(Short Answer)
4.8/5  (33)
(33)
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
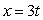 ,
, 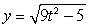
(Multiple Choice)
4.9/5  (34)
(34)
(a) Identify the type of conic by the discriminant, (b) transform the equation in x and y into an equation in X and Y (without an XY term) by rotating the x- and y-axes by an angle of θ to arrive at the new X- and Y-axes, and (c) graph the resulting equation (showing both sets of axes).
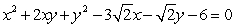
(Short Answer)
4.9/5  (33)
(33)
Showing 121 - 140 of 230
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)