Exam 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations
Exam 1: Functions and Their Graphs137 Questions
Exam 2: Polynomial and Rational Functions141 Questions
Exam 3: Exponential and Logarithmic Functions137 Questions
Exam 4: Trigonometric Functions of Angles261 Questions
Exam 5: Trigonometric Functions of Real Numbers151 Questions
Exam 6: Analytic Trigonometry267 Questions
Exam 7: Vectors, the Complex Plane, and Polar Coordinates225 Questions
Exam 8: Systems of Linear Equations and Inequalities181 Questions
Exam 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations230 Questions
Exam 10: Sequences and Series124 Questions
Exam 11: Limits: A Preview to Calculus122 Questions
Exam 12: Review: Equations and Inequalities244 Questions
Select questions type
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
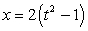 ,
, 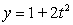
(Multiple Choice)
4.8/5  (38)
(38)
Graph the second-degree equation. (Hint: Transform the equation into an equation that contains no xy term.) 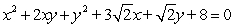
(Multiple Choice)
4.8/5  (29)
(29)
Graph the second-degree equation. (Hint: Transform the equation into an equation that contains no xy term.)
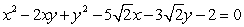
(Short Answer)
4.8/5  (31)
(31)
If the xy-coordinate axes are rotated 60°, find the XY coordinates of the point (x, y) =
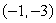 .
.
(Short Answer)
4.8/5  (31)
(31)
Identify the conic section given by the following equation as a parabola, ellipse, circle, or hyperbola.
18x2 - 20x - 13y2 + 15y + 10 = -8
(Multiple Choice)
4.9/5  (30)
(30)
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
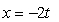 ,
, 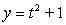
(Short Answer)
4.9/5  (42)
(42)
If the xy-coordinate axes are rotated 30°, find the XY coordinates of the point (x, y) =
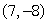 .
.
(Short Answer)
4.9/5  (33)
(33)
(a) Identify the type of conic by the discriminant, (b) transform the equation in x and y into an equation in X and Y (without an XY term) by rotating the x- and y-axes by an angle of θ to arrive at the new X- and Y-axes, and (c) graph the resulting equation (showing both sets of axes).
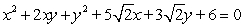
(Short Answer)
4.9/5  (39)
(39)
Graph each equation and find the point(s) of intersection.
X2 + y2 = 1
-x + y = 7
(Multiple Choice)
4.9/5  (36)
(36)
The difference of two numbers is 74 and the difference of their squares is 3700. Find the numbers.
(Short Answer)
4.8/5  (34)
(34)
Find the standard form of the ellipse with the following equation.
36x2 + 4y2 - 144x - 24y = -36
(Multiple Choice)
4.8/5  (29)
(29)
Find the standard form of the hyperbola with the following equation.
7x2 - 3y2 - 112x - 30y = -352
(Multiple Choice)
4.8/5  (27)
(27)
If the xy-coordinate axes are rotated 30°, find the XY coordinates of the point (x, y) =
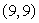 .
.
(Short Answer)
4.7/5  (31)
(31)
Solve the system of equations by applying the elimination method.
9x2 + 5y = 4
-9x2 - 5y = 4
(Multiple Choice)
4.9/5  (34)
(34)
Graph the second-degree equation. (Hint: Transform the equation into an equation that contains no xy term). 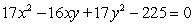
(Multiple Choice)
4.9/5  (33)
(33)
Recall that the flight of a projectile can be modeled with the parametric equations:
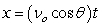 ,
, 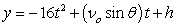 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 465 ft/sec at an angle of 33° with the horizontal. How far does the projectile travel (what is the horizontal distance), and what is the maximum altitude? Round to the nearest integer.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 465 ft/sec at an angle of 33° with the horizontal. How far does the projectile travel (what is the horizontal distance), and what is the maximum altitude? Round to the nearest integer.
(Short Answer)
4.7/5  (33)
(33)
Find the standard form of the equation of an ellipse with foci (2, 0) and (-2, 0), and vertices (6, 0) and (-6, 0).
(Short Answer)
4.8/5  (37)
(37)
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
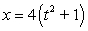 ,
, 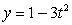
(Short Answer)
4.8/5  (43)
(43)
Showing 61 - 80 of 230
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)