Exam 9: Inference for Regression
Exam 1: Collecting Data68 Questions
Exam 2: Describing Data125 Questions
Exam 3: Confidence Intervals148 Questions
Exam 4: Hypothesis Tests119 Questions
Exam 5: Approximating With a Distribution74 Questions
Exam 6: Inference for Means and Proportions166 Questions
Exam 7: Chi-Square Tests for Categorical Variables47 Questions
Exam 8: Anova to Compare Means52 Questions
Exam 9: Inference for Regression123 Questions
Exam 10: Multiple Regression72 Questions
Exam 11: Probability Basics165 Questions
Select questions type
Use the following
Data were collected on GPA and number of Facebook friends for students in a small statistics class. Some summary statistics, partial output from the regression analysis, and a scatterplot of the data (with regression line) are provided. Assume that students in this class are typical of all students at the university.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
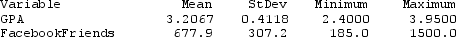 The regression equation is GPA = 3.830 - 0.000919 FacebookFriends
The regression equation is GPA = 3.830 - 0.000919 FacebookFriends

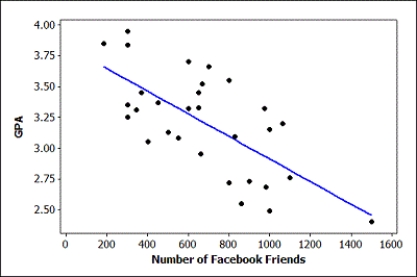 -Use the provided output to construct and interpret a 90% confidence interval for the mean GPA of all students with 800 Facebook friends.
-Use the provided output to construct and interpret a 90% confidence interval for the mean GPA of all students with 800 Facebook friends.
(Essay)
4.8/5  (45)
(45)
Use the following
Data were collected on GPA and number of Facebook friends for students in a small statistics class. Some summary statistics, partial output from the regression analysis, and a scatterplot of the data (with regression line) are provided. Assume that students in this class are typical of all students at the university.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
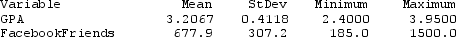 The regression equation is GPA = 3.830 - 0.000919 FacebookFriends
The regression equation is GPA = 3.830 - 0.000919 FacebookFriends

 -Use the information in the computer output to compute the standard error of the slope, SE. Round the answer to six decimal places.
-Use the information in the computer output to compute the standard error of the slope, SE. Round the answer to six decimal places.
(Essay)
4.7/5  (35)
(35)
Use the following
Data were collected on the age (in years) and price (in thousands of dollars) of a random sample of 25 used Hyundai Elantras. A scatterplot of the data (with regression line) and computer output from a regression analysis are provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
The regression equation is Price = 15.3 - 1.71 Age
 S = 1.37179 R-Sq = 88.9% R-Sq(adj) = 88.4%
Predicted Values for New Observations
S = 1.37179 R-Sq = 88.9% R-Sq(adj) = 88.4%
Predicted Values for New Observations
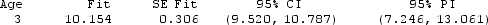
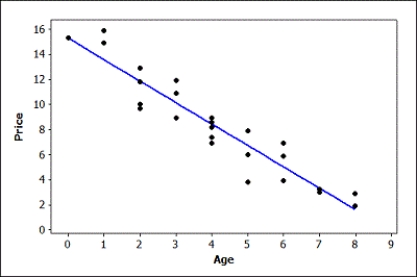 -Construct and interpret a 90% confidence interval for the population slope.
-Construct and interpret a 90% confidence interval for the population slope.
(Essay)
4.9/5  (43)
(43)
Use the following
A quantitatively savvy, young couple is interested in purchasing a home in northern New York. They collected data on 48 houses that had recently sold in the area. They want to predict the selling price of homes (in thousands of dollars) based on the size of the home (in square feet).
The regression equation is Price (in thousands) = 17.1 + 0.0643 Size (sq. ft.)
 S = 48.5733 R-Sq = 37.5% R-Sq(adj) = 36.1%
Predicted Values for New Observations
S = 48.5733 R-Sq = 37.5% R-Sq(adj) = 36.1%
Predicted Values for New Observations
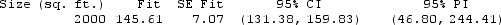
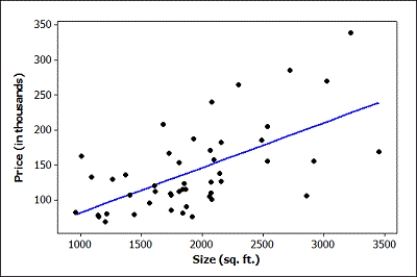 -What is the estimated slope in this regression model? Interpret the slope in context.
-What is the estimated slope in this regression model? Interpret the slope in context.
(Essay)
4.9/5  (40)
(40)
Use the following
In recent years, fast food restaurants have been required to publish nutrition information about the foods they serve. Nutrition information about a random sample of 15 McDonald's lunch/dinner menu items (excluding sides and drinks) was obtained from their website. We wish to use the total fat content (in grams) to better understand the number of calories in the lunch/dinner menu items at McDonald's. Computer output from a regression analysis and a scatterplot (with regression line) of the data are provided.
Use two decimal places when reporting the results from any calculations, unless otherwise specified.
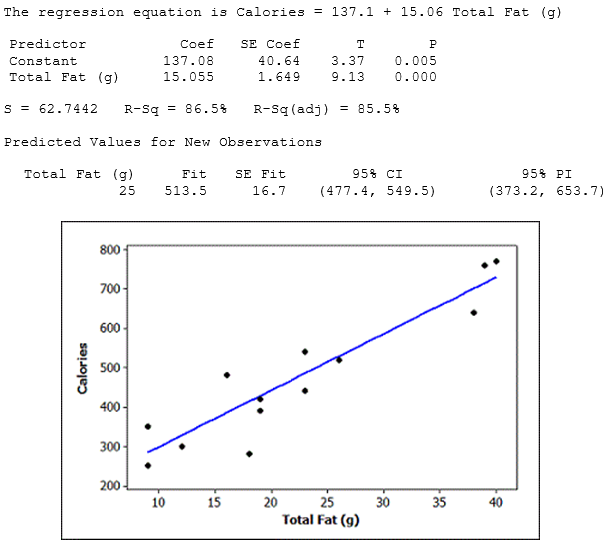 -Use the computer output to provide and interpret a 95% interval for the mean number of calories in all McDonald's lunch/menu items with 25 total grams of fat.
-Use the computer output to provide and interpret a 95% interval for the mean number of calories in all McDonald's lunch/menu items with 25 total grams of fat.
(Essay)
4.8/5  (37)
(37)
Use the following
Students in a small statistics course wanted to investigate if forearm length (in cm) was useful for predicting foot length (in cm). The data they collected are displayed in the provided scatterplot (with regression), and the computer output from the analysis is provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
The regression equation is Foot (cm) = 9.22 + 0.574 Forearm (cm)

 Predicted Values for New Observations
Predicted Values for New Observations
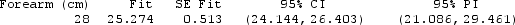
 -Based on the output, provide and interpret a 95% confidence interval for the mean foot length for all individuals with a forearm that is 28 cm. long.
-Based on the output, provide and interpret a 95% confidence interval for the mean foot length for all individuals with a forearm that is 28 cm. long.
(Essay)
4.7/5  (30)
(30)
Use the following
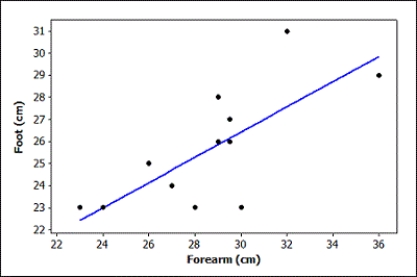
Data were collected on the mileage (in thousands of miles) and price (in thousands of dollars) of a random sample of used Hyundai Elantras. A scatterplot of the data (with regression line), some summary statistics, and partial computer output from a regression analysis are provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
 The regression equation is Price = 13.8 - 0.0912 Mileage
The regression equation is Price = 13.8 - 0.0912 Mileage

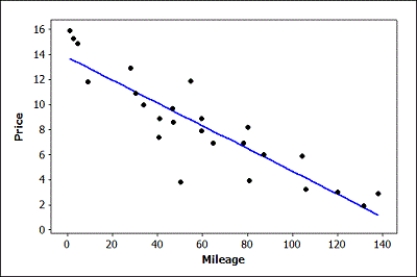 -Use the scatterplot to determine whether we should have any strong concerns about the conditions being met for using a linear model with these data. Explain briefly.
-Use the scatterplot to determine whether we should have any strong concerns about the conditions being met for using a linear model with these data. Explain briefly.
(Essay)
4.8/5  (35)
(35)
Use the following
In recent years, fast food restaurants have been required to publish nutrition information about the foods they serve. Nutrition information about a random sample of McDonald's lunch/dinner menu items (excluding sides and drinks) was obtained from their website. We wish to use the sodium content (in milligrams) to better understand the number of calories in the lunch/dinner menu items at McDonald's. Some summary statistics, partial computer output from a regression analysis, and a scatterplot (with regression line) of the data are provided.
Use two decimal places when reporting the results from any calculations, unless otherwise specified.
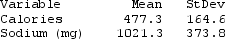 The regression equation is Calories = 99.69 + 0.3698 Sodium (mg)
The regression equation is Calories = 99.69 + 0.3698 Sodium (mg)

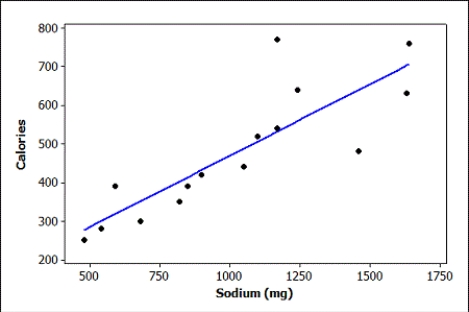 -Is the linear model effective at predicting the number of calories in lunch/dinner menu items at McDonald's? Use the information from the computer output (and = 0.05) for this test. Include all details of the test.
-Is the linear model effective at predicting the number of calories in lunch/dinner menu items at McDonald's? Use the information from the computer output (and = 0.05) for this test. Include all details of the test.
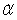
(Essay)
4.9/5  (36)
(36)
Use the following
In recent years, fast food restaurants have been required to publish nutrition information about the foods they serve. Nutrition information about a random sample of McDonald's lunch/dinner menu items (excluding sides and drinks) was obtained from their website. We wish to use the sodium content (in milligrams) to better understand the number of calories in the lunch/dinner menu items at McDonald's. Some summary statistics, partial computer output from a regression analysis, and a scatterplot (with regression line) of the data are provided.
Use two decimal places when reporting the results from any calculations, unless otherwise specified.
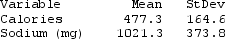 The regression equation is Calories = 99.69 + 0.3698 Sodium (mg)
The regression equation is Calories = 99.69 + 0.3698 Sodium (mg)

 -Use the scatterplot to determine whether we should have any serious concerns about the conditions being met for using a linear model with these data. Explain briefly.
-Use the scatterplot to determine whether we should have any serious concerns about the conditions being met for using a linear model with these data. Explain briefly.
(Essay)
4.9/5  (39)
(39)
Use the following
Students in a small statistics course wanted to investigate if forearm length (in cm) was useful for predicting foot length (in cm). The data they collected are displayed in the provided scatterplot (with regression), and the computer output from the analysis is provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
The regression equation is Foot (cm) = 9.22 + 0.574 Forearm (cm)

 Predicted Values for New Observations
Predicted Values for New Observations
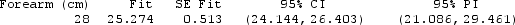
 -Use the ANOVA table to compute and interpret R2.
-Use the ANOVA table to compute and interpret R2.
(Essay)
4.9/5  (44)
(44)
Use the following
A quantitatively savvy, young couple is interested in purchasing a home in northern New York. They collected data on houses that had recently sold in the area. They want to predict the selling price of homes (in thousands of dollars) based on the age of the home (in years). Some summary statistics, partial regression output, and a scatterplot of the relationship (with regression line) are provided.
Use two decimal places when reporting the results from any calculations, unless otherwise specified.
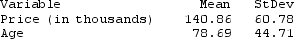 The regression equation is Price (in thousands) = 193 - 0.665 Age
Analysis of Variance
The regression equation is Price (in thousands) = 193 - 0.665 Age
Analysis of Variance

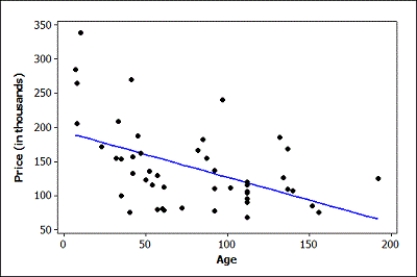 -What is the estimated slope in this regression model? Interpret the slope in context.
-What is the estimated slope in this regression model? Interpret the slope in context.
(Essay)
4.9/5  (38)
(38)
Use the following
Students in a small statistics course wanted to investigate if forearm length (in cm) was useful for predicting foot length (in cm). The data they collected are displayed in the provided scatterplot (with regression), and the computer output from the analysis is provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
The regression equation is Foot (cm) = 9.22 + 0.574 Forearm (cm)

 Predicted Values for New Observations
Predicted Values for New Observations
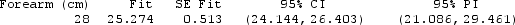
 -The correlation between foot length and forearm length is 0.7389. Compute and interpret R2 for this regression model.
-The correlation between foot length and forearm length is 0.7389. Compute and interpret R2 for this regression model.
(Essay)
4.9/5  (37)
(37)
Use the following
Computer output from a regression analysis is provided.
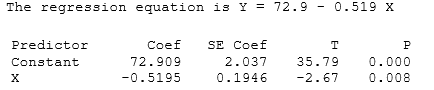 -The sample size in this situation is n = 157. What are the degrees of freedom for constructing a confidence interval for, or performing a test about, the population slope?
-The sample size in this situation is n = 157. What are the degrees of freedom for constructing a confidence interval for, or performing a test about, the population slope?
(Multiple Choice)
4.9/5  (32)
(32)
Use the following
A quantitatively savvy, young couple is interested in purchasing a home in northern New York. They collected data on 48 houses that had recently sold in the area. They want to predict the selling price of homes (in thousands of dollars) based on the size of the home (in square feet).
The regression equation is Price (in thousands) = 17.1 + 0.0643 Size (sq. ft.)
 S = 48.5733 R-Sq = 37.5% R-Sq(adj) = 36.1%
Predicted Values for New Observations
S = 48.5733 R-Sq = 37.5% R-Sq(adj) = 36.1%
Predicted Values for New Observations
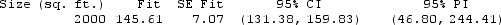
 -Write down the equation of the least squares line and use it to predict the selling price of a home that is 1,742 square feet in size.
-Write down the equation of the least squares line and use it to predict the selling price of a home that is 1,742 square feet in size.
(Essay)
4.9/5  (46)
(46)
Use the following
Students in a small statistics course wanted to investigate if forearm length (in cm) was useful for predicting foot length (in cm). The data they collected are displayed in the provided scatterplot (with regression), and the computer output from the analysis is provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
The regression equation is Foot (cm) = 9.22 + 0.574 Forearm (cm)

 Predicted Values for New Observations
Predicted Values for New Observations
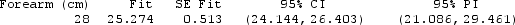
 -What is the estimated slope in this regression model? Interpret the slope in context.
-What is the estimated slope in this regression model? Interpret the slope in context.
(Essay)
4.8/5  (35)
(35)
Use the following
Data were collected on the mileage (in thousands of miles) and price (in thousands of dollars) of a random sample of used Hyundai Elantras. A scatterplot of the data (with regression line), some summary statistics, and partial computer output from a regression analysis are provided.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
 The regression equation is Price = 13.8 - 0.0912 Mileage
The regression equation is Price = 13.8 - 0.0912 Mileage

 -Write down the equation of the least squares line and use it to predict the price of a used Hyundai Elantra with 50,000 miles.
-Write down the equation of the least squares line and use it to predict the price of a used Hyundai Elantra with 50,000 miles.
(Essay)
4.9/5  (39)
(39)
Use the following
Computer output from a regression analysis is provided.
 -What is the sample slope for this model?
-What is the sample slope for this model?
(Multiple Choice)
4.8/5  (43)
(43)
Use the following to answer questions :
Computer output from a regression analysis is provided.
 -What is the p-value for testing if the slope in the population is different from zero?
-What is the p-value for testing if the slope in the population is different from zero?
(Multiple Choice)
4.8/5  (37)
(37)
Use the following
Data were collected on GPA and number of Facebook friends for students in a small statistics class. Some summary statistics, partial output from the regression analysis, and a scatterplot of the data (with regression line) are provided. Assume that students in this class are typical of all students at the university.
Use three decimal places when reporting the results from any calculations, unless otherwise specified.
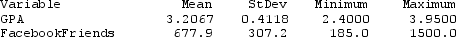 The regression equation is GPA = 3.830 - 0.000919 FacebookFriends
The regression equation is GPA = 3.830 - 0.000919 FacebookFriends

 -The correlation between GPA and number of Facebook friends is -0.686. Use the correlation and = 0.05 to test for a negative linear association between GPA and number of Facebook friends. Include all details of the test.
-The correlation between GPA and number of Facebook friends is -0.686. Use the correlation and = 0.05 to test for a negative linear association between GPA and number of Facebook friends. Include all details of the test.
(Essay)
4.8/5  (38)
(38)
Use the following
In recent years, fast food restaurants have been required to publish nutrition information about the foods they serve. Nutrition information about a random sample of McDonald's lunch/dinner menu items (excluding sides and drinks) was obtained from their website. We wish to use the sodium content (in milligrams) to better understand the number of calories in the lunch/dinner menu items at McDonald's. Some summary statistics, partial computer output from a regression analysis, and a scatterplot (with regression line) of the data are provided.
Use two decimal places when reporting the results from any calculations, unless otherwise specified.
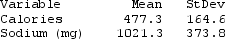 The regression equation is Calories = 99.69 + 0.3698 Sodium (mg)
The regression equation is Calories = 99.69 + 0.3698 Sodium (mg)

 -Use the provided output to compute and interpret R2.
-Use the provided output to compute and interpret R2.
(Essay)
4.8/5  (38)
(38)
Showing 61 - 80 of 123
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)