Exam 6: Integer Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis51 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet89 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling73 Questions
Exam 6: Integer Linear Programming73 Questions
Exam 7: Goal Programming and Multiple Objective Optimization62 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis77 Questions
Exam 10: Discriminant Analysis60 Questions
Exam 11: Time Series Forecasting116 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory80 Questions
Exam 14: Decision Analysis101 Questions
Exam 15: Project Management Online63 Questions
Select questions type
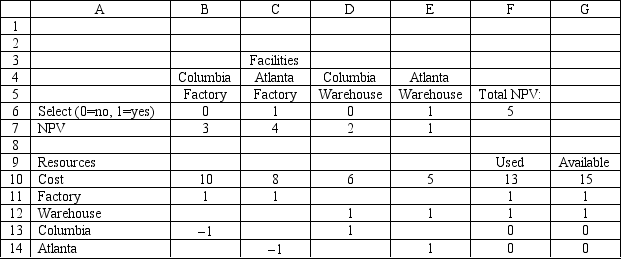
A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $15 million to invest.
Formulate the ILP for this problem.

(Essay)
4.9/5  (38)
(38)
Variables, which are not required to assume strictly integer values are referred to as
(Multiple Choice)
4.8/5  (39)
(39)
A research director must pick a subset of research projects to fund over the next five years. He has five candidate projects, not all of which cover the entire five-year period. Although the director has limited funds in each of the next five years, he can carry over unspent research funds into the next year. Additionally, up to $30K can be carried out of the five-year planning period. The following table summarizes the projects and budget available to the research director.
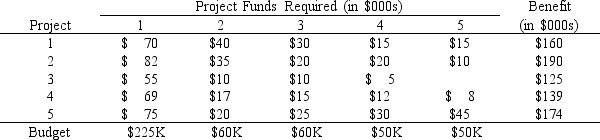 Define the ILP formulation for this capital budgeting problem.
Define the ILP formulation for this capital budgeting problem.
(Essay)
4.9/5  (38)
(38)
How is the integer tolerance factor set in the Risk Solver Platform (RSP)?
(Multiple Choice)
4.7/5  (30)
(30)
A cellular phone company wants to locate two new communications towers to cover 4 regions. The company wants to minimize the cost of installing the two towers. The regions that can be covered by each tower site are indicated by a 1 in the following table:
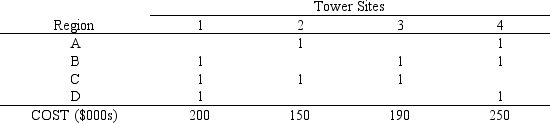 Formulate the ILP for this problem.
Formulate the ILP for this problem.
(Essay)
4.8/5  (42)
(42)
A company has four projects, numbered 1 through 4. If any project is selected for implementation, each lower-numbered project must also be selected for implementation. Formulate the constraints to enforce these conditions.
(Essay)
4.8/5  (38)
(38)
If a company selects Project 1 then it must also select either Project 2 or Project 3. Which of the following constraints enforces this condition?
(Multiple Choice)
4.8/5  (46)
(46)
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table. 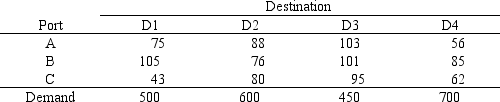 The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
Formulate the ILP for this problem capturing the ship choice of ports and the supply-to-demand transportation from the ports to the destinations.
The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
Formulate the ILP for this problem capturing the ship choice of ports and the supply-to-demand transportation from the ports to the destinations.
(Essay)
4.7/5  (27)
(27)
If a company selects either of Project 1 or Project 2 (or both), then either Project 3 or Project 4 (or both) must also be selected. Which of the following constraints enforce this condition?
(Multiple Choice)
5.0/5  (30)
(30)
A manufacturing company has costs associated with production preparation and with per unit production. The per unit production costs are referred to as
(Multiple Choice)
4.9/5  (40)
(40)
A company produces three products which must be painted, assembled, and inspected. The machinery must be cleaned and adjusted before each batch is produced. They want to maximize their profits for the amount of operating time they have. The unit profit and setup cost per batch are:
 The operation time per unit and total operating hours available are:
The operation time per unit and total operating hours available are:
 Formulate the ILP for this problem.
Formulate the ILP for this problem.
(Essay)
4.7/5  (33)
(33)
Consider the constraint X3 + X4 + X5 + X6 + X7 27
Representing Air Express' Monday minimum worker requirement. Why was a " " used versus an "="?
(Multiple Choice)
5.0/5  (36)
(36)
A company produces three products which must be painted, assembled, and inspected. The machinery must be cleaned and adjusted before each batch is produced. They want to maximize their profits for the amount of operating time they have. The unit profit and setup cost per batch are:
 The operation time per unit and total operating hours available are:
The operation time per unit and total operating hours available are:
 Based on this ILP formulation of the problem and the optimal solution (X1, X2, X3) = (270, 0, 0), what values should appear in the shaded cells in the following Excel spreadsheet?
Xi = amount of product i produced
Yi = 1 if product i produced, 0 otherwise
Based on this ILP formulation of the problem and the optimal solution (X1, X2, X3) = (270, 0, 0), what values should appear in the shaded cells in the following Excel spreadsheet?
Xi = amount of product i produced
Yi = 1 if product i produced, 0 otherwise
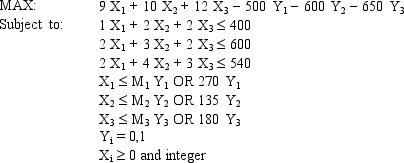
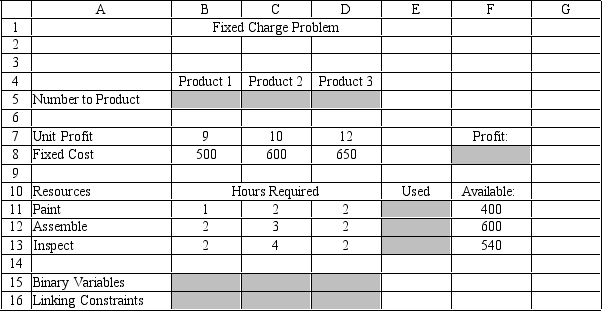
(Essay)
4.9/5  (37)
(37)
A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $15 million to invest.
 Based on this ILP formulation of the problem and the indicated optimal solution what values should go in cells B6:G14 of the following Excel spreadsheet?
Based on this ILP formulation of the problem and the indicated optimal solution what values should go in cells B6:G14 of the following Excel spreadsheet?
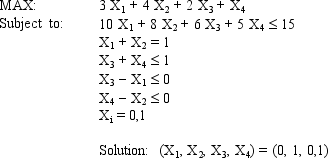
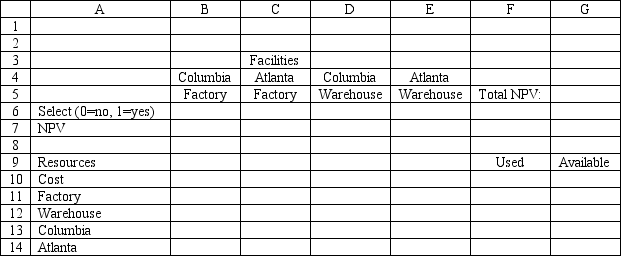
(Essay)
4.8/5  (38)
(38)
If a company produces Product 1, then it must produce at least 150 units of Product 1. Which of the following constraints enforces this condition?
(Multiple Choice)
4.9/5  (27)
(27)
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table. 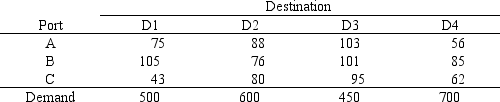 The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem.
The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem.

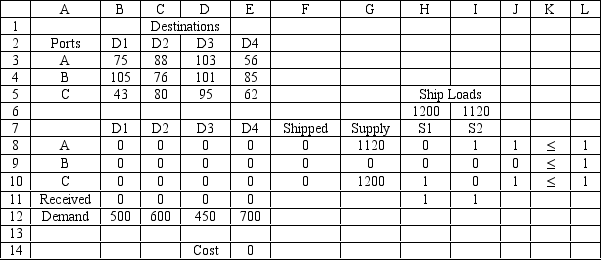 -Refer to Exhibit 6.2. What formula would go into cell E14?
-Refer to Exhibit 6.2. What formula would go into cell E14?
(Short Answer)
4.8/5  (30)
(30)
A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $16 million to invest.
 Based on this ILP formulation of the problem and the indicated optimal solution what formulas should go in cells F6:F14 of the following Excel spreadsheet?
Based on this ILP formulation of the problem and the indicated optimal solution what formulas should go in cells F6:F14 of the following Excel spreadsheet?
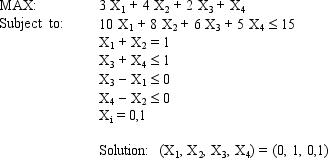
(Essay)
4.9/5  (28)
(28)
An investor has $500,000 to invest and wants to maximize the money they will receive at the end of one year. They can invest in condos, apartments and houses. The profit after one year, the cost and the number of units available are shown below.
Formulate the ILP for this problem.
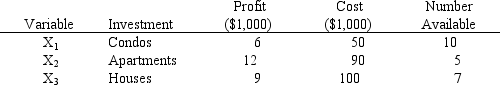
(Essay)
4.7/5  (36)
(36)
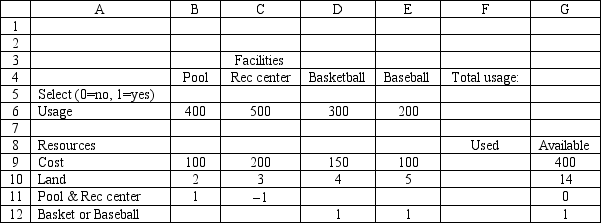
A small town wants to build some new recreational facilities. The proposed facilities include a swimming pool, recreation center, basketball court and baseball field. The town council wants to provide the facilities which will be used by the most people, but faces budget and land limitations. The town has $400,000 and 14 acres of land. The pool requires locker facilities which would be in the recreation center, so if the swimming pool is built the recreation center must also be built. Also the council has only enough flat land to build the basketball court or the baseball field. The daily usage and cost of the facilities (in $1,000) are shown below.
 Based on this ILP formulation of the problem what formulas should go in cells F5:F12 of the following Excel spreadsheet?
Based on this ILP formulation of the problem what formulas should go in cells F5:F12 of the following Excel spreadsheet?
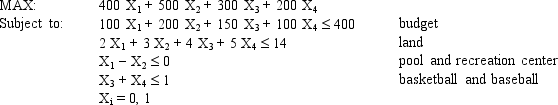
(Essay)
4.8/5  (37)
(37)
Showing 41 - 60 of 73
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)