Exam 7: Goal Programming and Multiple Objective Optimization
Exam 1: Introduction to Modeling and Decision Analysis51 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet89 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling73 Questions
Exam 6: Integer Linear Programming73 Questions
Exam 7: Goal Programming and Multiple Objective Optimization62 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis77 Questions
Exam 10: Discriminant Analysis60 Questions
Exam 11: Time Series Forecasting116 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory80 Questions
Exam 14: Decision Analysis101 Questions
Exam 15: Project Management Online63 Questions
Select questions type
A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000.
Formulate a goal programming model of this problem.
(Essay)
4.7/5  (43)
(43)
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.  Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
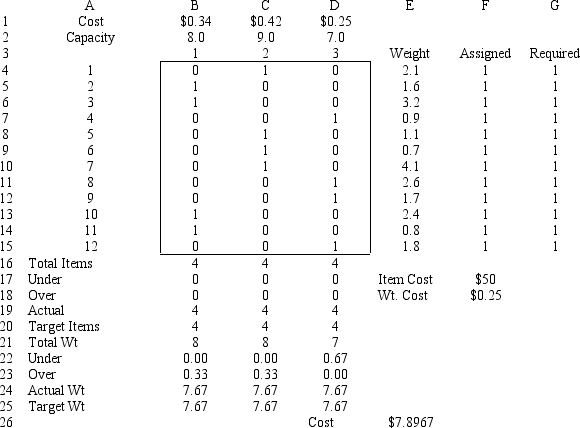 -Refer to Exhibit 7.4. What formulas should go in cell E26 of the spreadsheet?
-Refer to Exhibit 7.4. What formulas should go in cell E26 of the spreadsheet?
(Essay)
4.8/5  (34)
(34)
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following multi-objective linear programming (MOLP) has been solved in Excel.
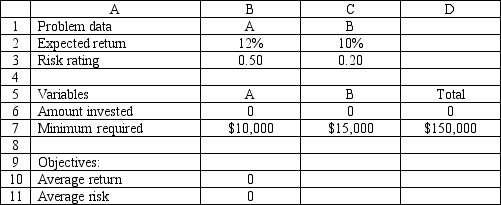 -Refer to Exhibit 7.2. Which cells are the changing cells in this model?
-Refer to Exhibit 7.2. Which cells are the changing cells in this model?
(Multiple Choice)
4.9/5  (34)
(34)
A constraint which represents a target value for a problem is called a
(Multiple Choice)
4.7/5  (33)
(33)
Which of the following formulas is a deviation-minimizing objective function for a goal programming problem?
(Multiple Choice)
4.9/5  (40)
(40)
A company wants to purchase large and small delivery trucks. The company wants to purchase about 10 large and 15 small trucks. Each large truck costs $30,000 and has a 10 ton capacity. Each small truck costs $20,000 and has a 7 ton capacity. The company wants to have about 200 tons of capacity and spend about $600,000.
Based on the following goal programming formulation, associated solution, and spreadsheet model, what formulas should go in cells D6:E6, B9:E9, and B16 of the spreadsheet?
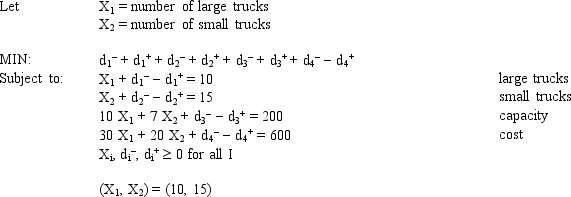
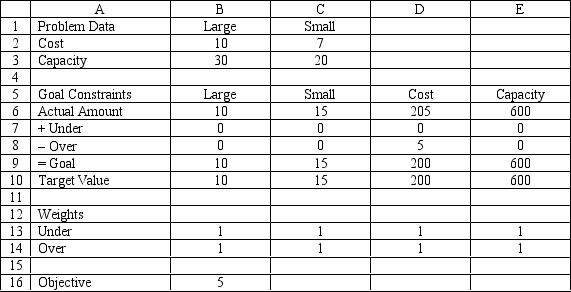
(Essay)
4.9/5  (38)
(38)
Exhibit 7.4
The following questions are based on the problem below.
Robert Gardner runs a small, local-only delivery service. His fleet consists of three smaller panel trucks. He recently accepted a contract to deliver 12 shipping boxes of goods for delivery to 12 different customers. The box weights are: 210, 160, 320, 90, 110, 70, 410, 260, 170, 240, 80 and 180 for boxes 1 through 12, respectively. Since each truck differs each truck has different load capacities as given below:
 Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.
Robert would like each truck equally loaded, both in terms of number of boxes and in terms of total weight, while minimizing his shipping costs. Assume a cost of $50 per item for trucks carrying extra boxes and $0.10 per pound cost for trucks carrying less weight.
The following integer goal programming formulation applies to his problem.
Y1 = weight loaded in truck 1; Y2 = weight loaded in truck 2; Y3 = weight loaded in truck 3;
Xi,j = 0 if truck i not loaded with box j; 1 if truck i loaded with box j.  Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
Given the following spreadsheet solution of this integer goal programming formulation, answer the following questions.
 -Refer to Exhibit 7.4. Given the solution indicated in the spreadsheet, which trucks, if any, are under an equal weight amount, and which trucks are over an equal weight amount?
-Refer to Exhibit 7.4. Given the solution indicated in the spreadsheet, which trucks, if any, are under an equal weight amount, and which trucks are over an equal weight amount?
(Essay)
4.8/5  (30)
(30)
A dietician wants to formulate a low cost, high calorie food product for a customer. The following information is available about the 2 ingredients which can be combined to make the food. The customer wants 1000 pounds of the food product and it must contain at least 250 pounds of Food 1 and 300 pounds of Food 2.
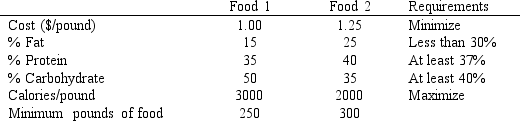 Formulate the MOLP for this problem.
Formulate the MOLP for this problem.
(Essay)
4.8/5  (31)
(31)
A dietician wants to formulate a low cost, high calorie food product for a customer. The following information is available about the 2 ingredients which can be combined to make the food. The customer wants 1000 pounds of the food product and it should contain 250 pounds of Food 1 and 300 pounds of Food 2. The final cost of the blend should be about $1.15 and contain about 2500 calories per pound. The percent of fat, protein, carbohydrate in each food is summarized below with the target values for the goals. The dietician would prefer the food product be low in fat while also high in protein and carbohydrates.
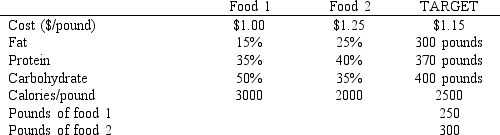 Formulate the GP for this problem
Formulate the GP for this problem
(Essay)
4.8/5  (39)
(39)
What is the meaning of the ti term in this objective function for a goal programming problem? 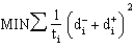
(Multiple Choice)
4.9/5  (23)
(23)
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.
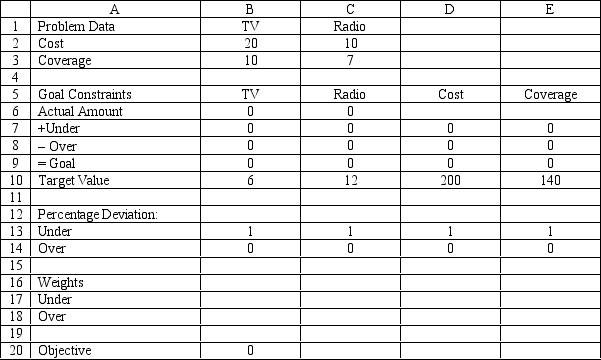 -Refer to Exhibit 7.1. If the company is very concerned about going over the $200,000 budget, which cell value should change and how should it change?
-Refer to Exhibit 7.1. If the company is very concerned about going over the $200,000 budget, which cell value should change and how should it change?
(Multiple Choice)
4.8/5  (33)
(33)
A company makes 2 products A and B from 2 resources, labor and material. The products have the following resource requirements and produce the accompanying profits. The available quantity of resources is also shown in the table.  Management has developed the following set of goals
Management has developed the following set of goals
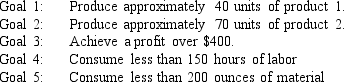 Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.
(Essay)
4.9/5  (48)
(48)
Exhibit 7.3
The following questions are based on the problem below.
An investor has $150,000 to invest in investments A and B. Investment A requires a $10,000 minimum investment, pays a return of 12% and has a risk factor of .50. Investment B requires a $15,000 minimum investment, pays a return of 10% and has a risk factor of .20. The investor wants to maximize the return while minimizing the risk of the portfolio. The following minimax formulation of the problem has been solved in Excel.
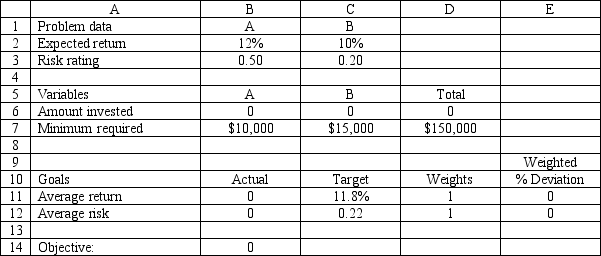 -Refer to Exhibit 7.3. Which value should the investor change, and in what direction, if he wants to reduce the risk of the portfolio?
-Refer to Exhibit 7.3. Which value should the investor change, and in what direction, if he wants to reduce the risk of the portfolio?
(Multiple Choice)
4.7/5  (43)
(43)
MINIMAX solutions to multi-objective linear programming (MOLP) problems are
(Multiple Choice)
4.9/5  (33)
(33)
The di+ variable indicates the amount by which each goal's target value is
(Multiple Choice)
4.8/5  (45)
(45)
A company needs to supply customers in 3 cities from its 3 warehouses. The supplies, demands and shipping costs are shown below.
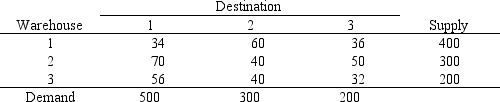 The company has identified the following goals:
The company has identified the following goals:
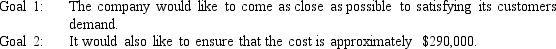 Formulate a goal programming model of this problem.
Formulate a goal programming model of this problem.
(Essay)
4.8/5  (38)
(38)
A manager wants to ensure that he does not exceed his budget by more than $1000 in a goal programming problem. If the budget constraint is the third constraint in the goal programming problem which of the following formulas will best ensure that the manager's objective is met?
(Multiple Choice)
4.8/5  (33)
(33)
Suppose that the first goal in a GP problem is to make 3 X1 + 4 X2 approximately equal to 36. Using the deviational variables d1- and d1+, the following constraint can be used to express this goal. 3 X1 + 4 X2 + d1- - d1+ = 36
If we obtain a solution where X1 = 6 and X2 = 2, what values do the deviational variables assume?
(Multiple Choice)
4.9/5  (37)
(37)
The following questions are based on the problem below.
A company wants to advertise on TV and radio. The company wants to produce about 6 TV ads and 12 radio ads. Each TV ad costs $20,000 and is viewed by 10 million people. Radio ads cost $10,000 and are heard by 7 million people. The company wants to reach about 140 million people, and spend about $200,000 for all the ads. The problem has been set up in the following Excel spreadsheet.
 -Refer to Exhibit 7.1. What formula goes in cell B9?
-Refer to Exhibit 7.1. What formula goes in cell B9?
(Multiple Choice)
4.9/5  (28)
(28)
Showing 21 - 40 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)