Exam 13: Queuing Theory

A store currently operates its service system with 1 operator. Arrivals follow a Poisson distribution and service times are exponentially distributed. The following spreadsheet has been developed for the system. -Refer to Exhibit 13.1. What is average amount of time spent waiting in line?

What is the mean arrival rate based on the following 8 arrival rate observations? Number of arrivals per hour: 6, 5, 3, 4, 7, 6, 4, 5

Which of the following is the typical operating characteristic for average time a unit spends waiting for service?

A computer printer in a large administrative office has a printer buffer (memory to store printing jobs) capacity of 3 jobs. If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later. There are so many users in this office that we can assume that there is an infinite calling population. Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print. Printing times are exponentially distributed. The following queuing analysis spreadsheet was developed from this information. -Refer to Exhibit 13.5. Based on this report what is the average number of jobs waiting to be printed?

An arrival process is memoryless if

A store currently operates its service system with 1 operator. Arrivals follow a Poisson distribution and service times are exponentially distributed. The following spreadsheet has been developed for the system. -Refer to Exhibit 13.1. What is the probability that a customer can go directly into service without waiting in line?

A doctor's office only has 8 chairs. The doctor's service times and customer inter-arrival times are exponentially distributed. What type of system is it?

A grocery clerk can serve 20 customers per hour on average and the service time follows an exponential distribution. What is the probability that a customer's service time is less than 2 minutes?

What is the service policy in the queuing systems presented in this chapter that is considered "fair" by the customers?

A company has recorded the following list of service rates (customers/hour) for one of its servers. What is the mean service time for this server? Customers / hour: 4, 4, 5, 6, 5, 4, 3, 4, 3, 5, 5, 6

A store currently operates its service system with 1 operator. Arrivals follow a Poisson distribution and service times are exponentially distributed. The following spreadsheet has been developed for the system. -Refer to Exhibit 13.1. What is the probability that a customer must wait in queue before being served?

A tax accountant has found that the time to serve a customer has a mean of 30 minutes (or 0.5 hours) and a standard deviation of 6 minutes (or 0.1 hours). Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals. The following queuing analysis spreadsheet was developed from this information. -Refer to Exhibit 13.7. Based on this report how long does a customer spend at the tax accountant's office?

To find steady-state values for the M/M/S queuing system, which of the following statements must be true about the arrival rate?

A barber shop has one barber who can give 12 haircuts per hour. Customers arrive at a rate of 8 customers per hour. Customer inter-arrival times and service times are exponentially distributed. The following queuing analysis spreadsheet was developed from this information. -Refer to Exhibit 13.2. What is the Kendall notation for this system?

Which of the following is the typical operating characteristic for average number of units in a queue?

A computer printer in a large administrative office has a printer buffer (memory to store printing jobs) capacity of 3 jobs. If the buffer is full when a user wants to print a file the user is told that the job cannot be printed and to try again later. There are so many users in this office that we can assume that there is an infinite calling population. Jobs arrive at the printer at a Poisson rate of 55 jobs per hour and take an average of 1 minute to print. Printing times are exponentially distributed. The following queuing analysis spreadsheet was developed from this information. -Refer to Exhibit 13.5. Based on this report how long does a computer user have to wait for his/her job to be completed?

A grocery store can serve an average of 360 customers per hour. The service times are exponentially distributed. The store has 4 checkout lines each of which serves 90 customers per hour. Customers arrive at the store at a Poisson rate of 240 customers per hour. The following queuing analysis spreadsheet was developed from this information. -Refer to Exhibit 13.4. Based on this report what percent of the time is a grocery clerk busy serving a customer?

A tax accountant has found that the time to serve a customer has a mean of 30 minutes (or 0.5 hours) and a standard deviation of 6 minutes (or 0.1 hours). Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals. The following queuing analysis spreadsheet was developed from this information. -Refer to Exhibit 13.7. Based on this report what is the probability that a customer does not have to wait for assistance with his or her taxes?

A company has recorded the following customer inter-arrival times and service times for 10 customers at one of its single teller service lines. Assume the data are exponentially distributed and the 10 data points represent a reasonable sample. 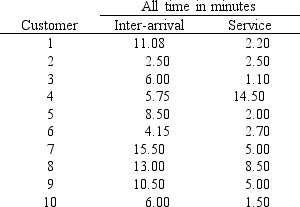-Refer to Exhibit 13.3. What is the average number of customers in the service line?

A jockey refers to