Exam 13: Queuing Theory
Exam 1: Introduction to Modeling and Decision Analysis51 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet89 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling73 Questions
Exam 6: Integer Linear Programming73 Questions
Exam 7: Goal Programming and Multiple Objective Optimization62 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization69 Questions
Exam 9: Regression Analysis77 Questions
Exam 10: Discriminant Analysis60 Questions
Exam 11: Time Series Forecasting116 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory80 Questions
Exam 14: Decision Analysis101 Questions
Exam 15: Project Management Online63 Questions
Select questions type
A tax accountant has found that the time to serve a customer has a mean of 30 minutes (or 0.5 hours) and a standard deviation of 6 minutes (or 0.1 hours). Customer arrivals follow a Poisson distribution with an average of 60 minutes between arrivals. The following queuing analysis spreadsheet was developed from this information.
 -Refer to Exhibit 13.7. What is the Kendall notation for this system?
-Refer to Exhibit 13.7. What is the Kendall notation for this system?
(Short Answer)
4.9/5  (35)
(35)
Which type of queuing system are you likely to encounter at a grocery store?
(Multiple Choice)
4.8/5  (42)
(42)
A barber shop has one barber, a Poisson arrival rate and exponentially distributed service times. What is the Kendall notation for this system?
(Multiple Choice)
4.8/5  (27)
(27)
A company has recorded the following list of service rates (customers/hour) for one of its servers. What is the mean service time for this server?
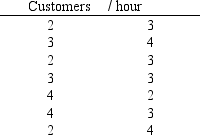
(Essay)
4.8/5  (45)
(45)
Customers arrive at a store randomly, following a Poisson distribution at an average rate of 90 per hour. How many customers would you expect to arrive in a 20 minute period?
(Short Answer)
4.8/5  (34)
(34)
A grocery store can serve an average of 360 customers per hour. The service times are exponentially distributed. The store has 4 checkout lines each of which serves 90 customers per hour. Customers arrive at the store at a Poisson rate of 240 customers per hour. The following queuing analysis spreadsheet was developed from this information.
 -Refer to Exhibit 13.4. Based on this report what is the average number of customers waiting for a checker?
-Refer to Exhibit 13.4. Based on this report what is the average number of customers waiting for a checker?
(Short Answer)
4.8/5  (33)
(33)
The standardized queuing system notation such as M/M/1 or M/G/2 is referred to as
(Multiple Choice)
4.8/5  (32)
(32)
What is the formula for the probability of x arrivals, p(x), under a Poisson distribution with arrival rate ?
(Multiple Choice)
4.7/5  (36)
(36)
Joe's Copy Center has 10 copiers. They break down at a rate of 0.02 copiers per hour and are sent to the service facility. What is the average arrival rate of broken copiers to the service facility?
(Multiple Choice)
4.9/5  (39)
(39)
Customers arrive at a store randomly, following a Poisson distribution at an average rate of 20 per hour. What is the probability of exactly 0, 1 2, and 3 arrivals in a 15 minute period?
(Essay)
4.9/5  (37)
(37)
Which of the following is a reason to employ queuing theory?
(Multiple Choice)
4.8/5  (29)
(29)
A store is considering adding a second clerk. The customer arrival rate at this new server will be
(Multiple Choice)
4.8/5  (34)
(34)
The university computer lab has 10 computers which are constantly being used by students. Users need help from the one lab assistant fairly often. Students ask for help at a Poisson rate of with an average of 4 requests per hour for any one computer. The assistant answers questions as quickly as possible and the service time follows an exponential distribution with mean of 1 minute per help session. The following queuing analysis spreadsheet was developed from this information.
 -Refer to Exhibit 13.6. Based on this report how much time do students spend getting help before they can resume work on their computers?
-Refer to Exhibit 13.6. Based on this report how much time do students spend getting help before they can resume work on their computers?
(Short Answer)
4.7/5  (35)
(35)
What is the mean arrival rate based on the following 10 arrival rate observations?

(Short Answer)
4.9/5  (34)
(34)
What is the formula for P(t - T) under the exponential distribution with rate ?
(Multiple Choice)
4.9/5  (41)
(41)
If a service system has a constant service time, Poisson arrival rates and 2 servers its Kendall notation is
(Multiple Choice)
4.8/5  (41)
(41)
Which type of queuing system are you likely to encounter at a Wendy's restaurant?
(Multiple Choice)
4.8/5  (34)
(34)
The customer service desk at Joe's Discount Electronics store receives 5 customers per hour on average. On average, each customer requires 10 minutes for service. The customer service desk is staffed by a single person. What is the average time a customer spends in the customer service area if modeled as an M/M/1 queuing system?
(Essay)
4.8/5  (40)
(40)
Showing 61 - 80 of 80
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)