Exam 8: Estimating Single Population Parameters

In discussing a confidence interval estimate for a population mean,is it acceptable to provide an interpretation like the following: "There is a 95 percent chance that μ lies in the range 20 to 40"?

Free

(Essay)

4.9/5

(33)

Question 1

Correct Answer:

Verified

No,this interpretation is not correct.As stated,it implies that μ is a random variable that can take on different values when in fact μ is a parameter and has a fixed value.The 95 percent confidence level indicates that of all possible confidence intervals constructed from a given size sample selected from the population,and using a z critical value associated with 95 percent confidence,95 percent of the intervals would contain the true population mean.The particular interval that we actually have computed (20 to 40)will either contain μ or it won't.

The t-distribution is used for the critical value when estimating a population proportion when the standard deviation of the population is not known.

Free

(True/False)

4.8/5

(34)

Question 2

Correct Answer:

Verified

False

The higher the level of confidence,the wider the confidence interval must be.

Free

(True/False)

4.9/5

(40)

Question 3

Correct Answer:

Verified

True

In a recent report to the supply-chain manager in a major electronics company,the report writer stated that with 90 percent confidence,the manufacturing lead time for a critical part is between 3.34 hours and 4.14 hours.Based on this,the sample mean that generated the confidence interval was 3.60.

(True/False)

4.8/5

(32)

Question 4

In an application to estimate the mean number of miles that downtown employees commute to work roundtrip each day,the following information is given: n = 20 = 4.33 S = 3.50 If the desired confidence level is 95 percent,the appropriate critical value is:

(Multiple Choice)

4.9/5

(27)

Question 5

A pilot sample is one that is used when a decision maker wishes to get an advance idea of what the mean of the population might be.

(True/False)

4.9/5

(35)

Question 6

When a decision maker determines the required sample size for estimating a population mean,a change in the confidence level will result in a change in the required sample size,provided that the margin of error is also modified accordingly.

(True/False)

4.8/5

(43)

Question 7

Assuming the population of interest is approximately normally distributed,construct a 95% confidence interval estimate for the population mean given the following values: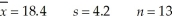

(Multiple Choice)

4.9/5

(35)

Question 8

The bottlers of a new fruit juice daily select a random sample of 12 bottles of the drink to estimate the mean quantity of juice in the bottles filled that day.On one such day,the following results were observed: = 12.03;s = 0.12.Based on this information,the margin of error associated with a 90 percent confidence interval estimate for the population mean is 1.7959 ounces.

(True/False)

4.9/5

(27)

Question 9

Under what circumstances would you wish to select a pilot sample?

(Essay)

4.9/5

(29)

Question 10

The national sales manager for a textbook publishing company wishes to estimate the mean number of books sold per college.She wishes to have her estimate be within ± 30 copies and wants a 95 percent confidence interval estimate.If a pilot sample of 30 schools gave a sample standard deviation equal to 60 books,the required total sample size is less than the pilot sample already taken.

(True/False)

4.9/5

(31)

Question 11

A 95 percent confidence interval estimate will have a margin of error that is approximately ±95 percent of the size of the population mean.

(True/False)

4.8/5

(29)

Question 12

A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph.From past information,it is known that the standard deviation of the population is 22 mph.The 95 percent confidence interval for μ is determined as (61.08,68.92).If we are to reduce the sample size to 100 (other factors remain unchanged),the 95 percent confidence interval for μ would:

(Multiple Choice)

4.8/5

(29)

Question 13

Two confidence interval estimates were developed from the same sample of a population.The wider interval will be the one that has the higher confidence level.

(True/False)

4.8/5

(47)

Question 14

The purpose of a pilot sample is:

(Multiple Choice)

4.8/5

(34)

Question 15

Which of the following will increase the width of a confidence interval (assuming that everything else remains constant)?

(Multiple Choice)

4.9/5

(34)

Question 16

A grocery store manager is interested in estimating the mean weight of apples received in a shipment.If she wishes to have the estimate be within ±.05 pound with 90 percent confidence,the sample size should be 103 apples if she believes that the standard deviation is .08 pound.

(True/False)

4.9/5

(46)

Question 17

The procurement manager for a large company wishes to estimate the proportion of parts from a supplier that are defective.She has selected a random sample of n = 200 incoming parts and has found 11 to be defective.Based on a 95 percent confidence level,the upper and lower limits for the confidence interval estimate are approximately 0.0234 to 0.0866.

(True/False)

4.7/5

(40)

Question 18

Determine the 90% confidence interval estimate for the population mean of a normal distribution given n = 100,σ = 121,and = 1,200.

(Multiple Choice)

4.8/5

(30)

Question 19

At issue is the proportion of people in a particular county who do not have health care insurance coverage.A simple random sample of 240 people was asked if they have insurance coverage,and 66 replied that they did not have coverage.Based on these sample data,determine the 95% confidence interval estimate for the population proportion.

(Multiple Choice)

4.8/5

(37)

Question 20

Showing 1 - 20 of 174

In discussing a confidence interval estimate for a population mean,is it acceptable to provide an interpretation like the following: "There is a 95 percent chance that μ lies in the range 20 to 40"?

The t-distribution is used for the critical value when estimating a population proportion when the standard deviation of the population is not known.

The higher the level of confidence,the wider the confidence interval must be.

In a recent report to the supply-chain manager in a major electronics company,the report writer stated that with 90 percent confidence,the manufacturing lead time for a critical part is between 3.34 hours and 4.14 hours.Based on this,the sample mean that generated the confidence interval was 3.60.

In an application to estimate the mean number of miles that downtown employees commute to work roundtrip each day,the following information is given: n = 20 = 4.33 S = 3.50 If the desired confidence level is 95 percent,the appropriate critical value is:

A pilot sample is one that is used when a decision maker wishes to get an advance idea of what the mean of the population might be.

When a decision maker determines the required sample size for estimating a population mean,a change in the confidence level will result in a change in the required sample size,provided that the margin of error is also modified accordingly.

Assuming the population of interest is approximately normally distributed,construct a 95% confidence interval estimate for the population mean given the following values:

Under what circumstances would you wish to select a pilot sample?

A 95 percent confidence interval estimate will have a margin of error that is approximately ±95 percent of the size of the population mean.

Two confidence interval estimates were developed from the same sample of a population.The wider interval will be the one that has the higher confidence level.

The purpose of a pilot sample is:

Which of the following will increase the width of a confidence interval (assuming that everything else remains constant)?

A grocery store manager is interested in estimating the mean weight of apples received in a shipment.If she wishes to have the estimate be within ±.05 pound with 90 percent confidence,the sample size should be 103 apples if she believes that the standard deviation is .08 pound.

Determine the 90% confidence interval estimate for the population mean of a normal distribution given n = 100,σ = 121,and = 1,200.

The Where,Why,and How of Data Collection

Graphs,Charts and Tablesdescribing Your Data

Describing Data Using Numerical Measures

Introduction to Probability

Discrete Probability Distributions

Introduction to Continuous Probability Distributions

Introduction to Sampling Distributions

Introduction to Hypothesis Testing

Estimation and Hypothesis Testing for Two Population Parameters

Hypothesis Tests and Estimation for Population Variances

Analysis of Variance

Goodness-Of-Fit Tests and Contingency Analysis

Introduction to Linear Regression and Correlation Analysis

Multiple Regression Analysis and Model Building

Analyzing and Forecasting Time-Series Data

Introduction to Nonparametric Statistics

Introduction to Quality and Statistical Process Control

Filters