Exam 18: Management of Waiting Lines
Exam 1: Introduction to Operations Management70 Questions
Exam 2: Competitiveness, Strategy, and Productivity73 Questions
Exam 3: Forecasting164 Questions
Exam 4: Product and Service Design77 Questions
Exam 5: Strategic Capacity Planning for Products and Services103 Questions
Exam 6: Process Selection and Facility Layout151 Questions
Exam 7: Work Design and Measurement151 Questions
Exam 8: Location Planning and Analysis80 Questions
Exam 9: Management of Quality102 Questions
Exam 10: Quality Control141 Questions
Exam 11: Aggregate Planning and Master Scheduling81 Questions
Exam 12: MRP and ERP89 Questions
Exam 13: Inventory Management162 Questions
Exam 14: Jit and Lean Operations88 Questions
Exam 15: Supply Chain Management89 Questions
Exam 16: Scheduling134 Questions
Exam 17: Project Management137 Questions
Exam 18: Management of Waiting Lines81 Questions
Exam 19: Linear Programming105 Questions
Exam 20: Extension 4: Reliability10 Questions
Exam 21: Extension 5: Decision Theory126 Questions
Exam 22: Extension 7: Learning Curves68 Questions
Exam 23: Extension 8: The Transportation Model20 Questions
Exam 24: Extension 10: Acceptance Sampling65 Questions
Exam 25: Extension 14: Maintenance38 Questions
Select questions type
Two troubleshooters handle service calls for 10 machines.The average time between service requirements is 18 days, and service time averages 2 days.Assume exponential distributions.While running, each machine can produce 1,500 pieces per day.Determine:
(A) the percentage of time troubleshooters are idle
(B) each machine's net productivity
(C) If troubleshooters represent a cost of $150 per day, and machine downtime cost is $600 per day, would another troubleshooter be justified? Explain.
(Essay)
5.0/5  (37)
(37)
Waiting lines occur even in under loaded systems because of variability in service rates and/or arrival rates.
(True/False)
4.7/5  (39)
(39)
A manager assembled the following information about an infinite source waiting line system: 5 servers, an arrival rate of 6 per hour, and a service time of 20 minutes.The manager has determined that the average number of customers waiting for service is 0.04.Determine each of the following:
(A) the system utilization
(B) the average waiting time in line in minutes
(C) the average time in the system
(D) the average number in the system
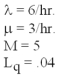
(Essay)
4.8/5  (36)
(36)
Offering an "early bird" special at a restaurant to reduce waiting times during peak hours is an example of ____________.
(Multiple Choice)
4.8/5  (43)
(43)
In a multi-channel system with multiple waiting lines, customers shifting among the waiting lines is an example of __________.
(Multiple Choice)
5.0/5  (35)
(35)
What is the average time that player's card holders wait to be seated?
(Multiple Choice)
5.0/5  (39)
(39)
What is the probability that a machine will have to wait for service with two operators?
(Multiple Choice)
4.9/5  (42)
(42)
If a manager increases system utilization (assuming no change in the customer arrival rate) what happens to the customer waiting time?
(Multiple Choice)
5.0/5  (33)
(33)
Servers, channels are described with many acronyms except _________.
(Multiple Choice)
4.7/5  (32)
(32)
The queuing models discussed in the text apply only to "steady state" conditions.Steady state exists only when customers arrive at a steady rate; that is, without any variability.
(True/False)
4.9/5  (33)
(33)
A multiple channel system has customers arriving at an average rate of five per hour and an average service time of forty minutes.The minimum number of servers for this system to be under loaded is:
(Multiple Choice)
4.9/5  (34)
(34)
The goal of waiting line management is to minimize waiting time.
(True/False)
4.7/5  (29)
(29)
The goal of waiting line management is to eliminate customer waiting lines.
(True/False)
4.9/5  (29)
(29)
Little's Law states that the number of people in a waiting line is the average customer arrival rate multiplied by the ________.
(Multiple Choice)
4.7/5  (34)
(34)
A department has 5 semiautomatic pieces of equipment which operate for an average of 79 minutes before they must be reloaded.The reloading operation takes an average of 21 minutes per machine.Assume exponential distributions.
(A) What is the minimum number of servers needed to keep the average downtime per cycle to less than 25 minutes?
(B) If 1 server is used, what percentage of time will the machine be down?
(Essay)
5.0/5  (32)
(32)
According to Little's Law, the number of people in line depends on the time of day that they arrive.
(True/False)
4.9/5  (39)
(39)
Which of the following would reduce perceived waiting times most dramatically in a doctor's office?
(Multiple Choice)
4.8/5  (36)
(36)
Showing 21 - 40 of 81
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)