Exam 7: Sampling and Sampling Distributions
Exam 1: Data and Statistics98 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Presentations64 Questions
Exam 3: Descriptive Statistics: Numerical Measures156 Questions
Exam 4: Introduction to Probability138 Questions
Exam 5: Discrete Probability Distributions122 Questions
Exam 6: Continuous Probability Distributions165 Questions
Exam 7: Sampling and Sampling Distributions131 Questions
Exam 8: Interval Estimation131 Questions
Exam 9: Hypothesis Tests133 Questions
Exam 10: Statistical Inference About Means and Proportions With Two Populations121 Questions
Exam 11: Inferences About Population Variances91 Questions
Exam 12: Tests of Goodness of Fit and Independence80 Questions
Exam 13: Analysis of Variance and Experimental Design113 Questions
Exam 14: Simple Linear Regression140 Questions
Exam 15: Multiple Regression106 Questions
Exam 16: Regression Analysis: Model Building75 Questions
Exam 17: Index Numbers52 Questions
Exam 18: Forecasting67 Questions
Exam 19: Nonparametric Methods81 Questions
Exam 20: Statistical Methods for Quality Control30 Questions
Exam 21: Decision Analysis65 Questions
Exam 22: Sample Survey63 Questions
Select questions type
Four hundred people were asked whether gun laws should be more stringent.Three hundred said "yes," and 100 said "no." The point estimate of the proportion in the population who will respond "yes" is
(Multiple Choice)
4.8/5  (34)
(34)
The SAT scores have an average of 1200 with a standard deviation of 60.A sample of 36 scores is selected.
a.What is the probability that the sample mean will be larger than 1224?
b.What is the probability that the sample mean will be less than 1230?
c.What is the probability that the sample mean will be between 1200 and 1214?
d.What is the probability that the sample mean will be greater than 1200?
e.What is the probability that the sample mean will be larger than 73.46?
(Essay)
4.9/5  (37)
(37)
The probability distribution of all possible values of the sample mean  Is
Is
(Multiple Choice)
4.8/5  (36)
(36)
In a local university,10% of the students live in the dormitories.A random sample of 100 students is selected for a particular study.
a.What is the probability that the sample proportion (the proportion living in the dormitories)is between 0.172 and 0.178?
b.What is the probability that the sample proportion (the proportion living in the dormitories)is greater than 0.025?
(Essay)
4.9/5  (39)
(39)
Random samples of size 17 are taken from a population that has 200 elements,a mean of 36,and a standard deviation of 8.Which of the following best describes the form of the sampling distribution of the sample mean for this situation?
(Multiple Choice)
4.9/5  (39)
(39)
Random samples of size 100 are taken from an infinite population whose population proportion is 0.2.The mean and standard deviation of the sample proportion are
(Multiple Choice)
4.9/5  (36)
(36)
A theorem that allows us to use the normal probability distribution to approximate the sampling distribution of sample means and sample proportions whenever the sample size is large is known as the
(Multiple Choice)
4.8/5  (25)
(25)
Exhibit 7-1
A random sample of 121 bottles of cologne showed an average content of 4 ounces.It is known that the standard deviation of the contents (i.e. ,of the population)is 0.22 ounces.
-Refer to Exhibit 7-1.In this problem the 0.22 is
(Multiple Choice)
4.9/5  (41)
(41)
A probability distribution for all possible values of a sample statistic is known as
(Multiple Choice)
5.0/5  (32)
(32)
A sample of 25 observations is taken from an infinite population.The sampling distribution of 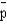 Is
Is
(Multiple Choice)
4.8/5  (40)
(40)
A population consists of 500 elements.We want to draw a simple random sample of 50 elements from this population.On the first selection,the probability of an element being selected is
(Multiple Choice)
5.0/5  (39)
(39)
The probability distribution of all possible values of the sample proportion 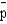 Is the
Is the
(Multiple Choice)
4.8/5  (41)
(41)
Exhibit 7-2
A random sample of 10 examination papers in a course,which was given on a pass or fail basis,showed the following scores.
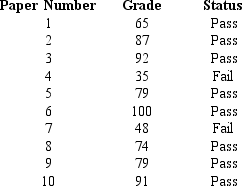 -Refer to Exhibit 7-2.The point estimate for the proportion of all students who passed the course is
-Refer to Exhibit 7-2.The point estimate for the proportion of all students who passed the course is
(Multiple Choice)
4.9/5  (37)
(37)
There are 8,000 students at the University of Tennessee at Chattanooga.The average age of all the students is 24 years with a standard deviation of 9 years.A random sample of 36 students is selected.
a.Determine the standard error of the mean.
b.What is the probability that the sample mean will be larger than 19.5?
c.What is the probability that the sample mean will be between 25.5 and 27 years?
(Essay)
4.7/5  (27)
(27)
Random samples of size 81 are taken from an infinite population whose mean and standard deviation are 200 and 18,respectively.The distribution of the population is unknown.The mean and the standard error of the mean are
(Multiple Choice)
4.8/5  (29)
(29)
A simple random sample of 100 observations was taken from a large population.The sample mean and the standard deviation were determined to be 80 and 12 respectively.The standard error of the mean is
(Multiple Choice)
4.8/5  (36)
(36)
A subset of a population selected to represent the population is
(Multiple Choice)
4.8/5  (38)
(38)
Showing 41 - 60 of 131
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)