Exam 17: Markov Processes

The probability that a system is in a particular state after a large number of periods is

A transition probability describes

The matrix of transition probabilities below deals with brand loyalty to Bark Bits and Canine Chow dog food. 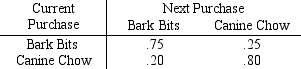a.What are the steady state probabilities? b.What is the probability that a customer will switch brands on the next purchase after a large number of periods?

The probability of going from state 1 in period 2 to state 4 in period 3 is

A city is served by three cable TV companies: Xcellent Cable,Your Cable,and Zephyr Cable.A survey of 1000 cable subscribers shows this breakdown of customers from the beginning to the end of August. a.Construct the transition matrix. b.What was each company's share of the market at the beginning and the end of the month? c.If the current trend continues what will the market shares be?

Bark Bits Company is planning an advertising campaign to raise the brand loyalty of its customers to .80. a.The former transition matrix is .75 .25 .20 .80 What is the new one? b.What are the new steady state probabilities? c.If each point of market share increases profit by $15000,what is the most you would pay for the advertising?

All Markov chains have steady-state probabilities.

A Markov chain cannot consist of all absorbing states.

A state,i,is an absorbing state if,when i = j,p_ij = 1.

If an absorbing state exists,then the probability that a unit will ultimately move into the absorbing state is given by the steady state probability.

The medical prognosis for a patient with a certain disease is to recover,to die,to exhibit symptom 1,or to exhibit symptom 2.The matrix of transition probabilities is 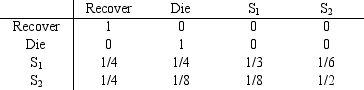a.What are the absorbing states? b.What is the probability that a patient with symptom 2 will recover?

Markov processes use historical probabilities.

Rent-To-Keep rents household furnishings by the month.At the end of a rental month a customer can: a)rent the item for another month,b)buy the item,or c)return the item.The matrix below describes the month-to-month transition probabilities for 32-inch stereo televisions the shop stocks. Next Month _{Rent Buy Return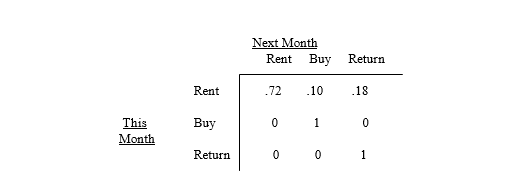} What is the probability that a customer who rented a TV this month will eventually buy it?

Henry,a persistent salesman,calls North's Hardware Store once a week hoping to speak with the store's buying agent,Shirley.If Shirley does not accept Henry's call this week,the probability she will do the same next week is .35.On the other hand,if she accepts Henry's call this week,the probability she will not do so next week is .20. a.Construct the transition matrix for this problem. b.How many times per year can Henry expect to talk to Shirley? c.What is the probability Shirley will accept Henry's next two calls if she does not accept his call this week? d.What is the probability of Shirley accepting exactly one of Henry's next two calls if she accepts his call this week?

The probability that the system is in state 2 in the 5th period is $\pi$ ₅(2).

On any particular day an individual can take one of two routes to work.Route A has a 25% chance of being congested,whereas route B has a 40% chance of being congested. The probability of the individual taking a particular route depends on his previous day's experience.If one day he takes route A and it is not congested,he will take route A again the next day with probability .8.If it is congested,he will take route B the next day with probability .7. On the other hand,if on a day he takes route B and it is not congested,he will take route B again the next day with probability .9.Similarly if route B is congested,he will take route A the next day with probability .6. a.Construct the transition matrix for this problem.(HINT: There are 4 states corresponding to the route taken and the congestion.The transition probabilities are products of the independent probabilities of congestion and next day choice. ) b.What is the long-run proportion of time that route A is taken?

For a situation with weekly dining at either an Italian or Mexican restaurant,

A state i is a transient state if there exists a state j that is reachable from i,but the state i is not reachable from state j.

A recent study done by an economist for the Small Business Administration investigated failures of small business.Failures were either classified as due to poor financing,poor management,or a poor product.The failure rates differed for new businesses (under one year old)versus established businesses (over one year old. ) As the result of the economist's study,the following probabilities were determined.For new businesses the probability of failure due to financing was .15,due to management .20,and due to product .05.The corresponding probabilities for established businesses were .10,.06,and .03 respectively. a.Determine a five-state Markov Chain transition matrix with states for new,established,and each of the three failure states.Write it in the form of I,O,R,and Q submatrices. b.Determine the probability that a new business will survive during the next three years. c.What proportion of new businesses eventually fail due to: (1)poor financing? (2)poor management? (3)poor product?

State j is an absorbing state if p_ij = 1.