Exam 6: Continuous Probability Distributions

The average starting salary of this year's graduates of a large university (LU) is $25,000 with a standard deviation of $5,000. Furthermore, it is known that the starting salaries are normally distributed. a.What is the probability that a randomly selected LU graduate will have a starting salary of at least $31,000? b.Individuals with starting salaries of less than $12,200 receive a low income tax break. What percentage of the graduates will receive the tax break? c.What are the minimum and the maximum starting salaries of the middle 95% of the LU graduates? d.If 68 of the recent graduates have salaries of at least $35,600, how many students graduated this year from this university?

The standard deviation of a standard normal distribution

Given that Z is a standard normal random variable. What is the value of Z if the area to the right of Z is 0.1401?

A major department store has determined that its customers charge an average of $500 per month, with a standard deviation of $80. Assume the amounts of charges are normally distributed. a.What percentage of customers charges more than $380 per month? b.What percentage of customers charges less than $340 per month? c.What percentage of customers charges between $644 and $700 per month?

The time it takes a mechanic to change the oil in a car is exponentially distributed with a mean of 5 minutes. a.What is the probability density function for the time it takes to change the oil? b.What is the probability that it will take a mechanic less than 6 minutes to change the oil? c.What is the probability that it will take a mechanic between 3 and 5 minutes to change the oil? d.What is the variance of the time it takes to change the oil?

The monthly earnings of computer systems analysts are normally distributed with a mean of $4,300. If only 1.07 percent of the systems analysts have a monthly income of more than $6,140, what is the value of the standard deviation of the monthly earnings of the computer systems analysts?

The length of time it takes students to complete a statistics examination is uniformly distributed and varies between 40 and 60 minutes. a.Find the mathematical expression for the probability density function. b.Compute the probability that a student will take between 45 and 50 minutes to complete the examination. c.Compute the probability that a student will take no more than 40 minutes to complete the examination. d.What is the expected amount of time it takes a student to complete the examination? e. What is the variance for the amount of time it takes a student to complete the examination?

A professor at a local university noted that the grades of her students were normally distributed with a mean of 78 and a standard deviation of 10. a.The professor has informed us that 16.6 percent of her students received grades of A. What is the minimum score needed to receive a grade of A? b.If 12.1 percent of her students failed the course and received F's, what was the maximum score among those who received an F? c.If 33 percent of the students received grades of B or better (i.e., A's and B's), what is the minimum score of those who received a B?

Exhibit 6-8 The life expectancy of a particular brand of tire is normally distributed with a mean of 40,000 and a standard deviation of 5,000 miles. -Refer to Exhibit 6-8. What is the probability that a randomly selected tire will have a life of at least 47,500 miles?

"DRUGS R US" is a large manufacturer of various kinds of liquid vitamins. The quality control department has noted that the bottles of vitamins marked 6 ounces vary in content with a standard deviation of 0.3 ounces. Assume the contents of the bottles are normally distributed. a.What percentage of all bottles produced contains more than 6.51 ounces of vitamins? b.What percentage of all bottles produced contains less than 5.415 ounces? c.What percentage of bottles produced contains between 5.46 to 6.495 ounces? d.Ninety-five percent of the bottles will contain at least how many ounces? e. What percentage of the bottles contains between 6.3 and 6.6 ounces?

The Body Paint, an automobile body paint shop, has determined that the painting time of automobiles is uniformly distributed and that the required time ranges between 45 minutes to 1 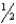hours. a.Give a mathematical expression for the probability density function. b.What is the probability that the painting time will be less than or equal to one hour? c.What is the probability that the painting time will be more than 50 minutes? d.Determine the expected painting time and its standard deviation.

Exhibit 6-4 f(x) =(1/10) e^-x/10 x 0 -Refer to Exhibit 6-4. The probability that x is between 3 and 6 is

The life expectancy of Timely brand watches is normally distributed with a mean of four years and a standard deviation of eight months. a.What is the probability that a randomly selected watch will be in working condition for more than five years? b.The company has a three-year warranty period on their watches. What percentage of their watches will be in operating condition after the warranty period? c.What is the minimum and the maximum life expectancy of the middle 95% of the watches? d.Ninety-five percent of the watches will have a life expectancy of at least how many months?

The z score for the standard normal distribution

In a standard normal distribution, the range of values of z is from

For a standard normal distribution, determine the probabilities of obtaining the following z values. It is helpful to draw a normal distribution for each case and show the corresponding area. a.Greater than zero b.Between -2.4 and -2.0 c.Less than 1.6 d.Between -1.9 to 1.7 e. Between 1.5 and 1.75

Larger values of the standard deviation result in a normal curve that is

The probability that a continuous random variable takes any specific value

The probability density function for a uniform distribution ranging between 2 and 6 is

A normal probability distribution