Exam 6: Continuous Probability Distributions
Exam 1: Data and Statistics104 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Presentations65 Questions
Exam 3: Descriptive Statistics: Numerical Measures162 Questions
Exam 4: Introduction to Probability146 Questions
Exam 5: Discrete Probability Distributions121 Questions
Exam 6: Continuous Probability Distributions165 Questions
Exam 7: Sampling and Sampling Distributions131 Questions
Exam 8: Interval Estimation131 Questions
Exam 9: Hypothesis Tests136 Questions
Exam 10: Comparisons Involving Means, Experimental Design and Analysis of Variance208 Questions
Exam 11: Comparisons Involving Proportions and a Test of Independence94 Questions
Exam 12: Simple Linear Regression140 Questions
Exam 13: Multiple Regression146 Questions
Select questions type
Exhibit 6-3
Consider the continuous random variable X, which has a uniform distribution over the interval from 20 to 28.
-Refer to Exhibit 6-3. The probability density function has what value in the interval between 20 and 28?
(Multiple Choice)
4.9/5  (39)
(39)
Given that Z is a standard normal random variable, what is the probability that -2.08 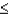 Z
Z 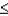 1.46?
1.46?
(Multiple Choice)
4.7/5  (28)
(28)
Exhibit 6-1
The assembly time for a product is uniformly distributed between 6 to 10 minutes.
-Refer to Exhibit 6-1. The probability of assembling the product in 7 minutes or more is
(Multiple Choice)
4.8/5  (37)
(37)
A major credit card company has determined that its customers charge an average of $280 per month on their accounts with a standard deviation of $20.
a.What percentage of the customers charges more than $275 per month?
b.What percentage of the customers charges less than $243 per month?
c.What percentage of the customers charges between $241 and $301.60 per month?
(Short Answer)
4.9/5  (48)
(48)
The price of a bond is uniformly distributed between $80 and $85.
a.What is the probability that the bond price will be at least $83?
b.What is the probability that the bond price will be between $81 to $90?
c.Determine the expected price of the bond.
d.Compute the standard deviation for the bond price.
(Short Answer)
4.9/5  (35)
(35)
In a standard normal distribution, the probability that Z is greater than zero is
(Multiple Choice)
4.9/5  (29)
(29)
Exhibit 6-2
The weight of football players is normally distributed with a mean of 200 pounds and a standard deviation of 25 pounds.
-Refer to Exhibit 6-2. The probability of a player weighing more than 241.25 pounds is
(Multiple Choice)
4.8/5  (31)
(31)
For a standard normal distribution, the probability of obtaining a z value between -2.4 to -2.0 is
(Multiple Choice)
4.8/5  (26)
(26)
Exhibit 6-2
The weight of football players is normally distributed with a mean of 200 pounds and a standard deviation of 25 pounds.
-Refer to Exhibit 6-2. What percent of players weigh between 180 and 220 pounds?
(Multiple Choice)
4.8/5  (33)
(33)
Given that Z is a standard normal random variable, what is the probability that -2.51 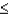 Z
Z 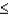 -1.53?
-1.53?
(Multiple Choice)
4.7/5  (44)
(44)
Exhibit 6-9
The average price of personal computers manufactured by MNM Company is $1,200 with a standard deviation of $220. Furthermore, it is known that the computer prices manufactured by MNM are normally distributed.
-Refer to Exhibit 6-9. What is the probability that a randomly selected computer will have a price of at least $1,530?
(Multiple Choice)
4.7/5  (35)
(35)
The time it takes to hand carve a guitar neck is uniformly distributed between 110 and 190 minutes.
a.What is the probability that a guitar neck can be carved between 95 and 165 minutes?
b.What is the probability that the guitar neck can be carved between 120 and 200 minutes?
c.Determine the expected completion time for carving the guitar neck.
d.Compute the standard deviation.
(Short Answer)
4.8/5  (30)
(30)
Exhibit 6-3
Consider the continuous random variable X, which has a uniform distribution over the interval from 20 to 28.
-Refer to Exhibit 6-3. The mean of X is
(Multiple Choice)
4.9/5  (38)
(38)
Exhibit 6-10
A professor at a local university noted that the grades of her students were normally distributed with a mean of 73 and a standard deviation of 11.
-Refer to Exhibit 6-10. The professor has informed us that 7.93 percent of her students received grades of A. What is the minimum score needed to receive a grade of A?
(Multiple Choice)
4.7/5  (32)
(32)
Z is a standard normal random variable. The P(Z > 2.11) equals
(Multiple Choice)
4.8/5  (36)
(36)
Z is a standard normal random variable. The P (-1.20 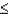 Z
Z 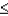 1.50) equals
1.50) equals
(Multiple Choice)
4.8/5  (44)
(44)
The function that defines the probability distribution of a continuous random variable is a
(Multiple Choice)
4.9/5  (23)
(23)
For a normal distribution, a negative value of z indicates
(Multiple Choice)
4.8/5  (34)
(34)
Showing 101 - 120 of 165
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)