Exam 6: Continuous Probability Distributions

Z is a standard normal random variable. The P (1.20 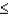Z 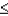1.85) equals

The ticket sales for events held at the new civic center are believed to be normally distributed with a mean of 12,000 and a standard deviation of 1,000. a.What is the probability of selling more than 10,000 tickets? b.What is the probability of selling between 9,500 and 11,000 tickets? c.What is the probability of selling more than 13,500 tickets?

Approximate the following binomial probabilities by the use of normal approximation. Twenty percent of students who finish high school do not go to college. What is the probability that in a sample of 80 high school students a.exactly 10 will not go to college? b.70 or more will go to college? c.fourteen or fewer will not go to college?

Which of the following is not a characteristic of the normal probability distribution?

Exhibit 6-3 Consider the continuous random variable X, which has a uniform distribution over the interval from 20 to 28. -Refer to Exhibit 6-3. The probability that X will take on a value of at least 26 is

Z is a standard normal random variable. Compute the following probabilities. a. P(-1.33 ≤ Z ≤ 1.67) b. P(1.23 ≤ Z ≤ 1.55) c. P(Z ≥ 2.32) d. P(Z ≥ -2.08) e. P(Z ≤ -1.08)

Twenty percent of the employees of a large company are female. Use the normal approximation of the binomial probabilities to answer the following questions. What is the probability that in a random sample of 80 employees a.exactly 16 will be female? b.14 or more will be female? c.15 or fewer will be female? d.18 or more will be female e. exactly 17 will be female?

The contents of soft drink bottles are normally distributed with a mean of twelve ounces and a standard deviation of one ounce. a.What is the probability that a randomly selected bottle will contain more than ten ounces of soft drink? b.What is the probability that a randomly selected bottle will contain between 9.5 and 11 ounces? c.What percentage of the bottles will contain less than 10.5 ounces of soft drink?

A local bank has determined that the daily balances of the checking accounts of its customers are normally distributed with an average of $280 and a standard deviation of $20. a.What percentage of its customers has daily balances of more than $275? b.What percentage of its customers has daily balances less than $243? c.What percentage of its customers' balances is between $241 and $301.60?

An airline has determined that 20% of its international flights are not on time. Use the normal approximation to the binomial distribution to answer the following questions. What is the probability that of the next 80 international flights a.Fifteen or less will not be on time? b.Eighteen or more will not be on time? c.Exactly 17 will not be on time?

The miles-per-gallon obtained by the 1995 model Z cars is normally distributed with a mean of 22 miles-per-gallon and a standard deviation of 5 miles-per-gallon. a.What is the probability that a car will get between 13.35 and 35.1 miles-per-gallon? b.What is the probability that a car will get more than 29.6 miles-per-gallon? c.What is the probability that a car will get less than 21 miles-per-gallon? d.What is the probability that a car will get exactly 22 miles-per-gallon?

The time between arrivals of customers at the drive-up window of a bank follows an exponential probability distribution with a mean of 10 minutes. a.What is the probability that the arrival time between customers will be 7 minutes or less? b.What is the probability that the arrival time between customers will be between 3 and 7 minutes?

The uniform, normal, and exponential distributions are

Scores on a recent national statistics exam were normally distributed with a mean of 80 and a standard deviation of 6. a.What is the probability that a randomly selected exam will have a score of at least 71? b.What percentage of exams will have scores between 89 and 92? c.If the top 2.5% of test scores receive merit awards, what is the lowest score eligible for an award? d.If there were 334 exams with scores of at least 89, how many students took the exam?

Given that Z is a standard normal random variable, what is the value of Z if the area to the left of Z is 0.119?

The uniform probability distribution is used with

Exhibit 6-5 The travel time for a college student traveling between her home and her college is uniformly distributed between 40 and 90 minutes. -Refer to Exhibit 6-5. The probability that she will finish her trip in 80 minutes or less is

The average price of cell phones manufactured by Ahmadi, Inc. is $98 with a standard deviation of $12. Furthermore, it is known that the prices of the cell phones manufactured by Ahmadi are normally distributed. a.What percentage of cell phones produced by Ahmadi, Inc. will have prices of at least $120.20? b.Cell phones with prices of at least 81.80 will get a free gift. What percentage of the cell phones will be eligible for the free gift? c.What are the minimum and the maximum values of the middle 95% of cell phone prices? d.If 7,218 of the Ahmadi cell phones were priced at least $119.00, how many cell phones were produced by Ahmadi, Inc.?

The salaries of the employees of a corporation are normally distributed with a mean of $25,000 and a standard deviation of $5,000. a.What is the probability that a randomly selected employee will have a starting salary of at least $31,000? b.What percentage of employees has salaries of less than $12,200? c.What are the minimum and the maximum salaries of the middle 95% of the employees? d.If sixty-eight of the employees have incomes of at least $35,600, how many individuals are employed in the corporation?

Exhibit 6-1 The assembly time for a product is uniformly distributed between 6 to 10 minutes. -Refer to Exhibit 6-1. The standard deviation of assembly time (in minutes) is approximately