Exam 10: Comparisons Involving Means, Experimental Design and Analysis of Variance

A recent Time magazine reported the following information about a sample of workers in Germany and the United States. 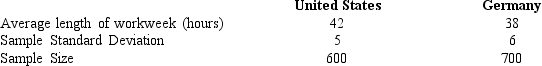We want to determine whether or not there is a significant difference between the average workweek in the United States and the average workweek in Germany. a.State the null and the alternative hypotheses. b.Compute the test statistic. c.Compute the p-value. What is your conclusion?

In an analysis of variance problem involving 3 treatments and 10 observations per treatment, SSE = 399.6. The MSE for this situation is

Random samples of several days' sales of handguns per day in three different states are shown below. We are interested in determining whether or not there is a significant difference in the average sales of guns in the three states a.Compute the overall mean. b.State the null and alternative hypotheses to be tested. c.Show the complete ANOVA table for this test including the test statistic. d.The null hypothesis is to be tested at 95% confidence. Determine the critical value for this test. What do you conclude? e. Determine the p-value and use it for the test.

In order to estimate the difference between the average yearly salaries of top managers in private and governmental organizations, the following information was gathered. Develop an interval estimate for the difference between the average salaries of the two sectors. Let $\alpha$ = .05.

Two independent samples are drawn from two populations, and the following information is provided. We want to test the following hypotheses. 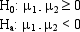a.Determine the degrees of freedom. b.Compute the test statistic. c.At 95% confidence, test the hypotheses. Assume the two populations are normally distributed and have equal variances.

A potential investor conducted a 144 day survey in each theater in order to determine the difference between the average daily attendance at the North Mall and South Mall theaters. The North Mall Theater averaged 630 patrons per day; while the South Mall Theater averaged 598 patrons per day. From past information, it is known that the variance for North Mall is 1,000; while the variance for the South Mall is 1,304. Develop a 95% confidence interval for the difference between the average daily attendance at the two theaters.

In a completely randomized experimental design, 11 experimental units were used for each of the 4 treatments. Part of the ANOVA table is shown below. Fill in the blanks in the above ANOVA table.

When developing an interval estimate for the difference between two sample means, with sample sizes of n₁ and n₂,

Exhibit 10-11 To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 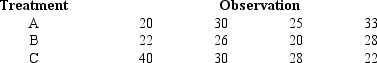-Refer to Exhibit 10-11. The null hypothesis is to be tested at the 1% level of significance. The p-value is

Exhibit 10-11 To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 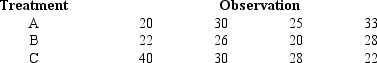-Refer to Exhibit 10-11. The null hypothesis for this ANOVA problem is

Exhibit 10-8 In order to determine whether or not there is a significant difference between the hourly wages of two companies, the following data have been accumulated. 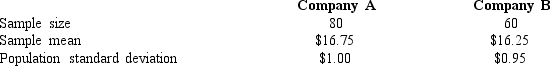-Refer to Exhibit 10-8. The null hypothesis

Exhibit 10-7 In order to estimate the difference between the average hourly wages of employees of two branches of a department store, the following data have been gathered. -Refer to Exhibit 10-7. A 95% interval estimate for the difference between the two population means is

Exhibit 10-14 Part of an ANOVA table is shown below. -Refer to Exhibit 10-14. The number of degrees of freedom corresponding to between treatments is

Random samples were selected from three populations. The data obtained are shown below. Please note that the sample sizes are not equal. a.Compute the overall mean. b.At 95% confidence using the critical value and p-value approach, test to see if there is a significant difference among the means.

Exhibit 10-11 To test whether or not there is a difference between treatments A, B, and C, a sample of 12 observations has been randomly assigned to the 3 treatments. You are given the results below. 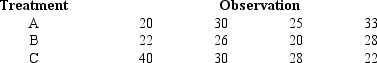-Refer to Exhibit 10-11. The mean square between treatments (MSTR) equals

Exhibit 10-15 The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations. -Refer to Exhibit 10-15. The number of degrees of freedom corresponding to within treatments is

Consider the following results for two samples randomly taken from two populations. a.Determine the degrees of freedom for the t-distribution. b.Develop a 95% confidence interval for the difference between the two population means.

In a completely randomized design involving three treatments, the following information is provided: 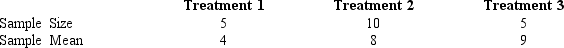The overall mean for all the treatments is

In order to determine whether or not a special tutoring service improves the scores of students in a Business Statistics examination, a sample of 6 students were given the exam before and after using the tutorial service. The results are shown below. Let d = Score After - Score Before. 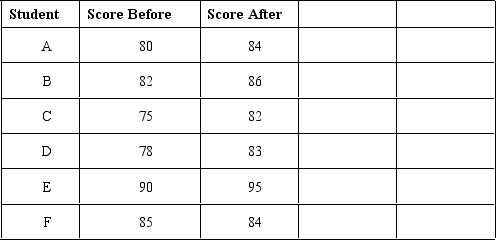At $\alpha$ = 0.10, test to see if the tutorial service actually increased scores on the examination.

The level of significance